3 Limited Expected Values

Overview. This section summarizes limited expected values for selected continuous distributions.

Functions

Limited Expected Value Functions

\[ \begin{matrix} \begin{array}{l|c} \hline \text{Distribuion} & \text{Function} \\ \hline \text{GB2} & \frac{\theta\Gamma(\tau+1)\Gamma(\alpha-1)}{\Gamma(\alpha)\Gamma(\tau)}\beta(\tau+1,\alpha-1;\frac{x}{x+\beta})+x[1-\beta(\tau,\alpha;\frac{x}{x+\beta})] \\ \hline \text{Burr} & \frac{\theta\Gamma(1+\frac{1}{\tau})\Gamma(\alpha-\frac{1}{\gamma})}{\Gamma(\alpha)}\beta(1+\frac{1}{\gamma},\alpha-\frac{1}{\gamma};1-\frac{1}{1+(x/\theta)^\gamma})+x\Big(\frac{1}{1+(x/\theta)^\gamma}\Big)^\alpha \\ \hline \text{Inverse Burr} & \frac{\theta\Gamma(1+(1/\gamma))\Gamma(1-(1/\gamma))}{\Gamma(\gamma)}\beta(\tau+\frac{1}{\gamma},1-\frac{1}{\gamma};\frac{(x/\theta)^\gamma}{1+(x/\theta)^\gamma})+x[1-\Big(\frac{(x/\theta)^\gamma}{1+(x/\theta)^\gamma}\Big)^\tau] \\ \hline \text{Pareto} & \\ \alpha=1 & -\theta \ln \Big(\frac{\theta}{x+\theta}\Big) \\ \alpha\neq1 & \frac{\theta}{\alpha-1}[1-\Big(\frac{\theta}{x+\theta}\Big)^{\alpha-1}] \\ \hline \text{Inverse Pareto} & \theta\tau\int^{x/(x+\theta)}_0~y^\tau(1-y)^{-1}dy+x[1-\Big(\frac{x}{x+\theta}\Big)^\tau] \\ \hline \text{Logistic} & \theta\Gamma_1(1+\frac{1}{\gamma})\Gamma(1-\frac{1}{\gamma})\beta(1+\frac{1}{\gamma},1-\frac{1}{\gamma};\frac{(x/\theta)^\gamma}{1+(x/\theta)^\gamma})+x(1-\frac{(x/\theta)^\gamma}{1+(x/\theta)^\gamma}) \\ \hline \text{Paralogistic} & \frac{\theta\Gamma(1+\frac{1}{\alpha})\Gamma(\alpha-\frac{1}{\alpha})}{\Gamma(\alpha)}\beta(1+\frac{1}{\alpha},\alpha-\frac{1}{\alpha};1-\frac{1}{1+(x/\theta)^\alpha})+x\Big(\frac{1}{1+(x/\theta)^\alpha}\Big)^\alpha \\ \hline \text{Inverse Paralogistic} & \frac{\theta\Gamma(\tau+\frac{1}{\tau})\Gamma(1-\frac{1}{\tau})}{\Gamma(\tau)}\beta(\tau+\frac{1}{\tau},1-\frac{1}{\tau};\frac{(x/\theta)^\tau}{1+(x/\theta)^\tau})+x[1-\Big(\frac{(x/\theta)^\tau}{1+(x/\theta)^\tau}\Big)^\tau] \\ \hline \text{Gamma} & \frac{\theta\Gamma(\alpha+1)}{\Gamma(\alpha)}\Gamma(\alpha+k;\frac{x}{\theta})+x[1-\Gamma(\alpha,\frac{x}{\theta})] \\ \hline \text{Inverse Gamma} & \frac{\theta\Gamma(\alpha-1)}{\Gamma(\alpha)}[1-\Gamma(\alpha-1;\frac{\theta}{x})]+x\Gamma(\alpha,\frac{\theta}{x}) \\ \hline \text{Weibull} & \theta\Gamma(1+\frac{1}{\tau})\Gamma(1+\frac{1}{\tau},\Big(\frac{x}{\theta}\Big)^\tau)+x*\exp(-(x/\theta)^\tau) \\ \hline \text{Inverse Weibull} & \theta\Gamma(1-\frac{1}{\tau})[1-\Gamma(1-\frac{1}{\tau};\Big(\frac{\theta}{x}\Big)^\tau)]+x[1-\exp(-(\theta/x)^\tau)] \\ \hline \text{Exponential} & \theta(1-\exp(-(x/\theta))) \\ \hline \text{Inverse Exponential} & \theta G(0;\frac{\theta}{x})+x(1-\exp(-(\theta/x))) \\ \hline \text{Lognormal} & \exp(\mu+\sigma^2/2)\Phi\Big(\frac{\ln (x)-\mu-\sigma^2}{\sigma}\Big)+x[1-\Phi\Big(\frac{\ln (x)-\mu}{\sigma}\Big)] \\ \hline \text{Inverse Gaussian} & x-\mu\Big(\frac{x-\mu}{\mu}\Big)\Phi\Big[\Big(\frac{x-\mu}{\mu}\Big)\Big(\frac{\theta}{x}\Big)^{1/2}\Big]-\mu\Big(\frac{x+\mu}{\mu}\Big)\exp\Big(\frac{2\theta}{\mu}\Big)\Phi\Big[-\Big(\frac{x+\mu}{\mu}\Big)\Big(\frac{\theta}{x}\Big)^{1/2}\Big] \\ \hline \text{Single-Parameter Pareto} & \frac{\alpha\theta}{\alpha-1}-\frac{\theta^\alpha}{(\alpha-1)x^{\alpha-1}} \\ \hline \text{Generalized Beta} & \frac{\theta\Gamma(a+b)\Gamma(a+\frac{1}{\tau})}{\Gamma(a)\Gamma(a+b+\frac{1}{\tau})}\beta(a+\frac{1}{\tau},b;\Big(\frac{x}{\theta}\Big)^\tau)+x\Big[1-\beta(a,b;\Big(\frac{x}{\theta}\Big)^\tau)\Big] \\ \hline \text{Beta} & \frac{\theta a}{(a+b)}\beta(a+1,b;\frac{x}{\theta})+x[1-\beta(a,b;\frac{x}{\theta})] \\ \hline \end{array} \end{matrix} \]

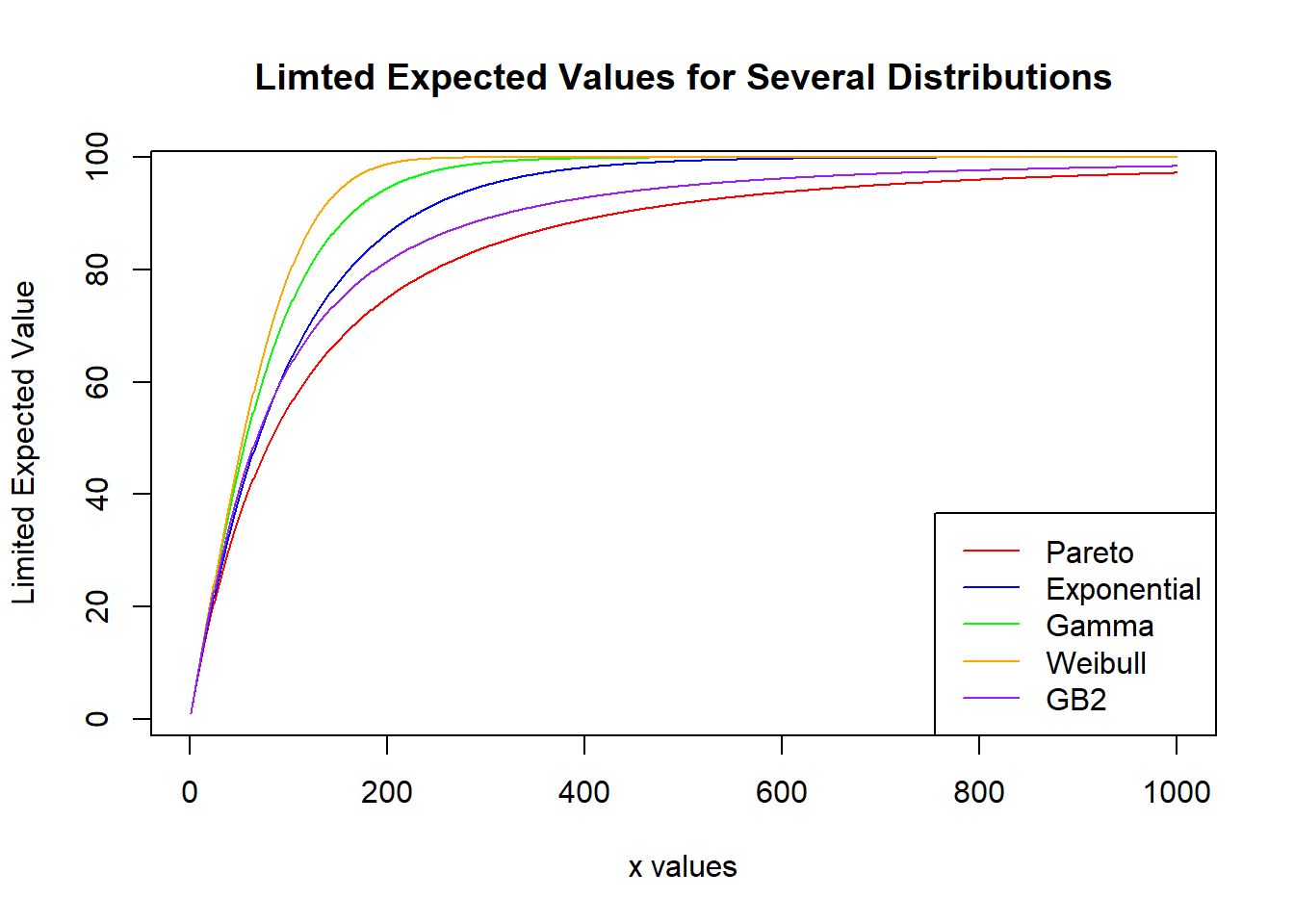
Illustrative Graph

Table of Limited Expected Values

\[ \begin{matrix} \begin{array}{l|c|c} \hline \text{Distribution} & \text{Parameters} & \mathrm{E}[x] & E[X\wedge100] & E[X\wedge250] & E[X\wedge500] &E[X\wedge1000] \\ \hline \text{Pareto} & \alpha = 3, \theta = 200 & 100 & 55.55 &80.25 & 91.84 & 97.22 \\ \hline \text{Exponential} & \theta = 100 & 100 & 63.21 & 91.79 & 99.33 & 99.99 \\ \hline \text{Gamma} & \alpha = 2, \theta = 50 & 100 & 72.93 & 97.64 & 99.97 & 100 \\ \hline \text{Weibull} & \tau=2, \theta=\frac{200}{\sqrt[]{\pi}} & 100 & 78.99 & 99.82 & 100 & 100 \\ \hline \text{GB2} & \alpha = 3,\tau=2,\theta = 100 & 100 & 62.50 & 86.00 & 94.91 & 98.42 \\ \hline \end{array} \end{matrix} \]