Chapter 3 Multiple Linear Regression

Chapter description

This chapter introduces linear regression in the case of several explanatory variables, known as multiple linear regression (MLR). Many basic linear regression concepts extend directly, including goodness of fit measures such as the coefficient of determination and inference using t-statistics. Multiple linear regression models provide a framework for summarizing highly complex, multivariate data. Because this framework requires only linearity in the parameters, we are able to fit models that are nonlinear functions of the explanatory variables, thus providing a wide scope of potential applications.

Term Life Data

Video Overhead Details

A Details. Demand for term life insurance

“Who buys insurance and how much do they buy?”

Companies have data on current customers
How do get info on potential (new) customers?

To understand demand, consider the Survey of Consumer Finances (SCF)

This is a nationally representative sample that contains extensive information on potential U.S. customers.
We study a random sample of 500 of the 4,519 households with positive income that were interviewed in the 2004 survey.
We now focus on n = 275 households that purchased term life insurance

B Details. Term life insurance summary statistics

We study y = face, the amount that the company will pay in the event of the death of the named insured.

We focus on k = 3 explanatory variables - annual income, - the number of years of education of the survey respondent and - the number of household members, numhh.

The data suggest that income and face are skewed so we also introduce logarithmic versions.

C Details. Summary statistics

#Term <- read.csv("CSVData\\term_life.csv", header = TRUE)
Term <- read.csv("https://assets.datacamp.com/production/repositories/2610/datasets/efc64bc2d78cf6b48ad2c3f5e31800cb773de261/term_life.csv", header = TRUE)
#  PICK THE SUBSET OF THE DATA CORRESPONDING TO TERM PURCHASE
Term1 <- subset(Term, subset = face > 0)
str(Term1)
head(Term1)

library(psych)
Term2 <- Term1[, c("education", "face", "income", "logface", "logincome", "numhh")]
#options(scipen = 100, digits = 4)
head(Term2)
describe(Term2)[,c(3,4,8,5,9,2)]

'data.frame':   275 obs. of  7 variables:
 $ education: int  16 9 16 17 11 16 17 16 14 12 ...
 $ face     : int  20000 130000 1500000 50000 220000 600000 100000 2500000 250000 50000 ...
 $ income   : int  43000 12000 120000 40000 28000 100000 112000 15000 32000 25000 ...
 $ logface  : num  9.9 11.8 14.2 10.8 12.3 ...
 $ logincome: num  10.67 9.39 11.7 10.6 10.24 ...
 $ numhh    : int  3 3 5 4 4 3 2 4 1 2 ...
 $ marstat  : int  1 1 1 1 2 1 1 1 0 1 ...
  education    face income   logface logincome numhh marstat
1        16   20000  43000  9.903488 10.668955     3       1
2         9  130000  12000 11.775290  9.392662     3       1
3        16 1500000 120000 14.220976 11.695247     5       1
4        17   50000  40000 10.819778 10.596635     4       1
6        11  220000  28000 12.301383 10.239960     4       2
8        16  600000 100000 13.304685 11.512925     3       1
  education    face income   logface logincome numhh
1        16   20000  43000  9.903488 10.668955     3
2         9  130000  12000 11.775290  9.392662     3
3        16 1500000 120000 14.220976 11.695247     5
4        17   50000  40000 10.819778 10.596635     4
6        11  220000  28000 12.301383 10.239960     4
8        16  600000 100000 13.304685 11.512925     3
               mean         sd    min    median       max   n
education     14.52       2.55   2.00     16.00 1.700e+01 275
face      747581.45 1674362.43 800.00 150000.00 1.400e+07 275
income    208974.62  824009.77 260.00  65000.00 1.000e+07 275
logface       11.99       1.87   6.68     11.92 1.645e+01 275
logincome     11.15       1.30   5.56     11.08 1.612e+01 275
numhh          2.96       1.49   1.00      3.00 9.000e+00 275

D Details. Scatter plots of income versus face in original and logarithmic units

par(mfrow = c(1, 2))
plot(Term2$income, Term2$face, xlab = "income", ylab = "face")
plot(Term2$logincome, Term2$logface, xlab = "log", ylab = "log face")

3.1 Method of least squares

In this section, you learn how to:

Interpret correlation coefficients by visualizing a scatterplot matrix
Fit a plane to data using the method of least squares
Predict an observation using a least squares fitted plane

3.1.1 Video

Video Overhead Details

A Details. Correlation table

round(cor(Term2), digits=3)

          education  face income logface logincome  numhh
education     1.000 0.244  0.163   0.383     0.343 -0.064
face          0.244 1.000  0.217   0.656     0.323  0.107
income        0.163 0.217  1.000   0.251     0.518  0.142
logface       0.383 0.656  0.251   1.000     0.482  0.288
logincome     0.343 0.323  0.518   0.482     1.000  0.179
numhh        -0.064 0.107  0.142   0.288     0.179  1.000

B Details. Scatterplot matrix

Term3 <- Term1[,c("numhh", "education", "logincome", "logface")]
pairs(Term3, upper.panel = NULL, gap = 0, cex.labels = 1.25)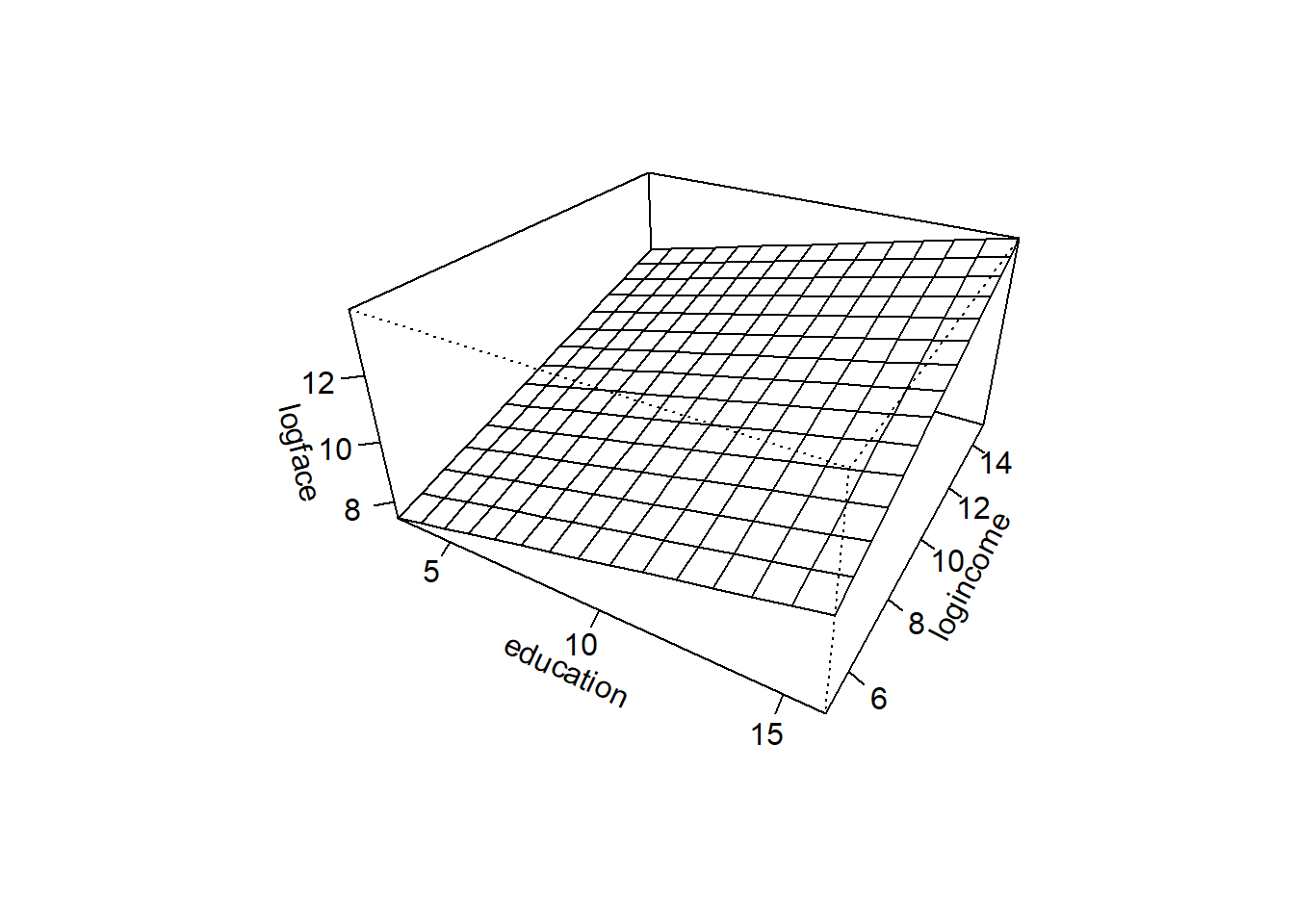

C Details. Visualizing a regression plane

education <- seq(3, 16, length = 15)
logincome <- seq(5, 15, length = 15)
f <- function(education,logincome){ 
  r <- 5 + 0.221*education + 0.354*logincome
}
logface <- outer(education, logincome, f)
persp(education, logincome, logface, theta = 30, 
      phi = 30, expand = 0.5, ticktype = "detailed")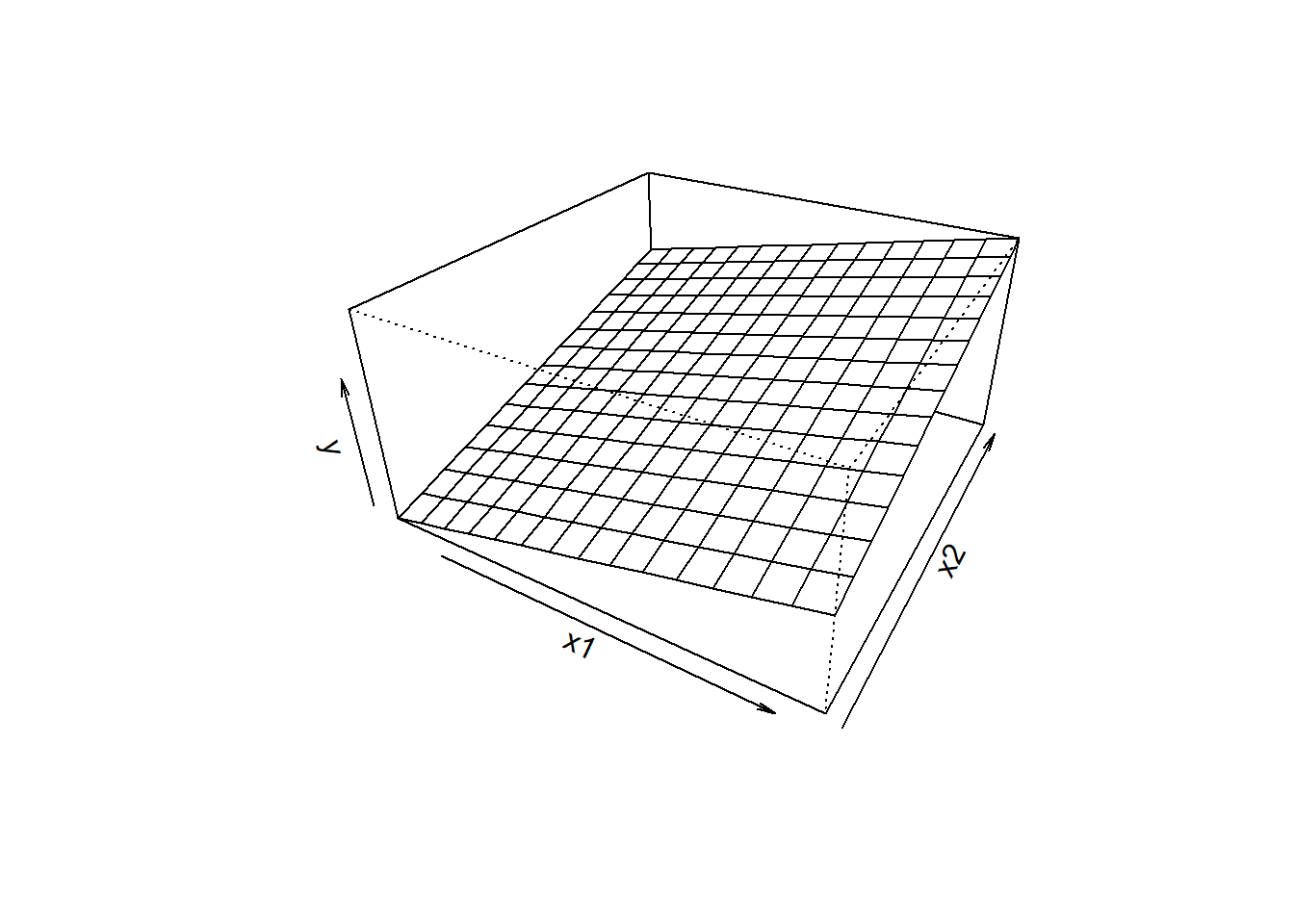

rm(education,logincome,logface)

education <- seq(3, 16, length = 15)
logincome <- seq(5, 15, length = 15)
f <- function(education,logincome){ 
  r <- 5 + 0.221*education + 0.354*logincome
}
logface <- outer(education, logincome, f)
persp(education, logincome, logface, theta = 30, 
      phi = 30, expand = 0.5, ticktype = "simple", #ticktype = "detailed", #
      xlab = "x1", ylab="x2",zlab="y", nticks = 1)

rm(education,logincome,logface)

D Details. Method of least squares

For observation $\{(y, x_1, \ldots, x_k)\}$, the height of the regression plane is \[b_0 + b_1 x_1 + \cdots + b_k x_k .\]
Thus, $y - (b_0 + b_1 x_1 + \cdots + b_k x_k)$ represents the deviation.
The sum of squared deviations is \[SS(b_0, \ldots, b_k) = \sum (y - (b_0 + b_1 x_1 + \cdots + b_k x_k))^2 .\]
The method of least squares – determine values of $b_0, \ldots, b_k$ that minimize $SS$.

E Details. Fit a multiple linear regression model

Term_mlr <- lm(logface ~ education + numhh + logincome, data = Term2)
round(coefficients(Term_mlr), digits=4)
newdata <- data.frame(logincome = log(60000), education = 12, numhh = 3)
exp(predict(Term_mlr, newdata))

(Intercept)   education       numhh   logincome 
     2.5841      0.2064      0.3060      0.4935 
       1 
90135.86

3.1.2 Exercise. Least squares and term life data

Assignment Text

The prior video introduced the Survey of Consumer Finances (SCF) term life data. A subset consisting of only those who purchased term life insurance, has already been read into a dataframe Term2.

Suppose that you wish to predict the amount of term life insurance that someone will purchase but are uneasy about the education variable. The SCF education variable is the number of completed years of schooling and so 12 corresponds to completing high school in the US. Your sense is that, for purposes of purchasing life insurance, high school graduates and those that attend college should be treated the same. So, in this exercise, your will create a new variable, education1, that is equal to years of education for those with education less than or equal to 12 and is equal to 12 otherwise.

Instructions

Use the pmin() function to create the education1 variable as part of the Term2 dataframe.
Check your work by examining summary statistics for the revised Term2 dataframe.
Examine correlations for the revised dataframe.
Using the method of least squares and the function lm(), fit a MLR model using logface as the dependent variables and using education, numhh, and logincome as explanatory variables.
With this fitted model and the function predict(), predict the face amount of insurance that someone with income of 40,000, 11 years of education, and 4 people in the household would purchase.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNUZXJtIDwtIHJlYWQuY3N2KFwiQ1NWRGF0YVxcXFx0ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvZWZjNjRiYzJkNzhjZjZiNDhhZDJjM2Y1ZTMxODAwY2I3NzNkZTI2MS90ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtMSA8LSBzdWJzZXQoVGVybSwgc3Vic2V0ID0gZmFjZSA+IDApXG5UZXJtMiA8LSBUZXJtMVssIGMoXCJlZHVjYXRpb25cIiwgXCJmYWNlXCIsIFwiaW5jb21lXCIsIFwibG9nZmFjZVwiLCBcImxvZ2luY29tZVwiLCBcIm51bWhoXCIpXSIsInNhbXBsZSI6IiMgQ3JlYXRlIHRoZSBgZWR1Y2F0aW9uMWAgdmFyaWFibGUgYXMgcGFydCBvZiB0aGUgYFRlcm0yYCBkYXRhZnJhbWUuXG5UZXJtMiRlZHVjYXRpb24xIDwtIHBtaW4oMTIsIFRlcm0yJGVkdWNhdGlvbilcblxuIyBDaGVjayB5b3VyIHdvcmsgYnkgZXhhbWluaW5nIHN1bW1hcnkgc3RhdGlzdGljcyBmb3IgdGhlIHJldmlzZWQgYFRlcm0yYCBkYXRhZnJhbWUuXG5zdW1tYXJ5KF9fXylcblxuIyBFeGFtaW5lIGNvcnJlbGF0aW9ucyBmb3IgdGhlIHJldmlzZWQgZGF0YWZyYW1lLlxucm91bmQoY29yKF9fXyksIGRpZ2l0cz0zKVxuXG4jIEZpdCBhIE1MUiBtb2RlbCB1c2luZyBgbG9nZmFjZWAgYXMgdGhlIGRlcGVuZGVudCB2YXJpYWJsZXMgYW5kIHVzaW5nIGBlZHVjYXRpb25gLCBgbnVtaGhgLCBhbmQgYGxvZ2luY29tZWAgYXMgZXhwbGFuYXRvcnkgdmFyaWFibGVzLlxuVGVybV9tbHIyIDwtIGxtKGxvZ2ZhY2UgfiBfX18gKyBudW1oaCArIGxvZ2luY29tZSwgZGF0YSA9IFRlcm0yKVxuXG4jIFByZWRpY3QgdGhlIGZhY2UgYW1vdW50IG9mIGluc3VyYW5jZSB0aGF0IHNvbWVvbmUgd2l0aCBpbmNvbWUgb2YgNDAsMDAwLCAxMSB5ZWFycyBvZiBlZHVjYXRpb24sIGFuZCA0IHBlb3BsZSBpbiB0aGUgaG91c2Vob2xkIHdvdWxkIHB1cmNoYXNlLlxubmV3ZGF0YSA8LSBkYXRhLmZyYW1lKGxvZ2luY29tZSA9IGxvZyg0MDAwMCksIGVkdWNhdGlvbjEgPSAxMSwgbnVtaGggPSA0KVxuZXhwKHByZWRpY3QoX19fLCBuZXdkYXRhKSkiLCJzb2x1dGlvbiI6IlRlcm0yJGVkdWNhdGlvbjEgPC0gcG1pbigxMiwgVGVybTIkZWR1Y2F0aW9uKVxuc3VtbWFyeShUZXJtMilcbnJvdW5kKGNvcihUZXJtMiksIGRpZ2l0cz0zKVxuVGVybV9tbHIyIDwtIGxtKGxvZ2ZhY2UgfiBlZHVjYXRpb24xICsgbnVtaGggKyBsb2dpbmNvbWUsIGRhdGEgPSBUZXJtMilcbm5ld2RhdGEgPC0gZGF0YS5mcmFtZShsb2dpbmNvbWUgPSBsb2coNDAwMDApLCBlZHVjYXRpb24xID0gMTEsIG51bWhoID0gNClcbmV4cChwcmVkaWN0KFRlcm1fbWxyMiwgbmV3ZGF0YSkpIiwic2N0IjoiZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwiVGVybTJcIikgJT4lIGNoZWNrX2NvbHVtbihcImVkdWNhdGlvbjFcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gYXNzaWduIHRoZSBtb2RpZmllZCBlZHVjYXRpb24gdmFyaWFibGUgdG8gYGVkdWNhdGlvbjFgIHVzaW5nIGBwbWluYC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwic3VtbWFyeVwiLCBub3RfY2FsbGVkX21zZz1cIk1ha2UgdXNlIG9mIGBzdW1tYXJ5YCB0byBmaW5kIHN1bW1hcnkgc3RhdHMgb2YgYFRlcm0yYC5cIikgJT4lICBjaGVja19hcmcoLiwgXCJvYmplY3RcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gcnVuIHN1bW1hcnkgb24gYFRlcm0yYC5cIikgXG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcInN1bW1hcnlcIiwgbm90X2NhbGxlZF9tc2c9XCJNYWtlIHVzZSBvZiBgc3VtbWFyeWAgdG8gZmluZCBzdW1tYXJ5IHN0YXRzIG9mIGBUZXJtMmAuXCIpICU+JSAgY2hlY2tfcmVzdWx0KCkgJT4lIGNoZWNrX2VxdWFsKClcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwicm91bmRcIiwgbm90X2NhbGxlZF9tc2c9XCJVc2UgYHJvdW5kYCB0byByb3VuZCB0aGUgY29ycmVsYXRpb25zIHRvIDMgZGlnaXRzLiBcIiApICU+JSB7XG4gIGNoZWNrX2FyZyguLCBcInhcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gY2FsbCBgcm91bmRgIG9uIHRoZSBjb3JyZWxhdGlvbnMgb2YgYWxsIHZhcmlhYmxlcyBpbiBgVGVybTJgLlwiKVxuICBjaGVja19hcmcoLiwgXCJkaWdpdHNcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJQbGVhc2Ugcm91bmQgdGhlc2UgY29ycmVsYXRpb25zIHRvIDMgZGlnaXRzLiBcIilcbn1cbmV4KCkgJT4lIGNoZWNrX29iamVjdChcIlRlcm1fbWxyMlwiLCB1bmRlZmluZWRfbXNnPVwiTWFrZSBzdXJlIHRvIGFzc2lnbiB5b3VyIGxpbmVhciBtb2RlbCB0byBgVGVybV9tbHIyYC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gbW9kZWwgYGxvZ2ZhY2VgIGJhc2VkIG9uIGBlZHVjYXRpb24xYCwgYG51bWhoYCwgYW5kIGBsb2dpbmNvbWVgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJsbVwiKSAlPiUge1xuICBjaGVja19hcmcoLiwgXCJmb3JtdWxhXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIG1vZGVsIGBsb2dmYWNlYCBiYXNlZCBvbiBgZWR1Y2F0aW9uMWAsIGBudW1oaGAsIGFuZCBgbG9naW5jb21lYC5cIilcbiAgY2hlY2tfYXJnKC4sIFwiZGF0YVwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBzcGVjaWZ5IG91ciBkYXRhIGNvbWVzIGZyb20gYFRlcm0yYC5cIilcbn1cbmV4KCkgJT4lIGNoZWNrX29iamVjdChcIm5ld2RhdGFcIiwgdW5kZWZpbmVkX21zZz1cIk1ha2Ugc3VyZSB0byBhc3NpZ24gb3VyIG5ldyBkYXRhIHRvIGBuZXdkYXRhYC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJtYWtlIHN1cmUgdG8gYXNzaWduIGVhY2ggY29sdW1uIG9mIHRoZSBkYXRhZnJhbWUgdG8gaXRzIHN0YXRlZCB2YWx1ZS4gXCIpXG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcImV4cFwiLCBub3RfY2FsbGVkX21zZz1cIk1ha2Ugc3VyZSB0byB0YWtlIHRoZSBleHBvbmVudGlhbCBvZiB5b3VyIHByZWRpY3Rpb24hIFwiKSAlPiUgY2hlY2tfcmVzdWx0KCkgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJUaGUgYXJndW1lbnQgaW4gYGV4cGAgc2hvdWxkIGJlIGNhbGxlZCBvbiB0aGUgcHJlZGljdGlvbi4gXCIpXG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcInByZWRpY3RcIiwgbm90X2NhbGxlZF9tc2c9XCJVdGlsaXplIGBwcmVkaWN0YCB0byBjcmVhdGUgcHJlZGljdGlvbnMgdXNpbmcgdGhpcyBtb2RlbC4gXCIpICU+JSB7XG4gIGNoZWNrX2FyZyguLCBcIm9iamVjdFwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBzcGVjaWZ5IHRoYXQgd2Ugd2FudCB0byBjcmVhdGUgcHJlZGljdGlvbnMgYmFzZWQgb2ZmIG9mIGBUZXJtMl9tbHIyYC5cIilcbiAgY2hlY2tfYXJnKC4sIFwibmV3ZGF0YVwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBzcGVjaWZ5IHdlIHdhbnQgdG8gbWFrZSBwcmVkaWN0aW9ucyBmb3IgdGhlIGRhdGEgd2UgZW50ZXJlZCBpbiBgbmV3ZGF0YWAuXCIpXG59XG5zdWNjZXNzX21zZyhcIkNvbmdyYXR1bGF0aW9ucyEgWW91IG5vdyBoYXZlIGV4cGVyaWVuY2UgZml0dGluZyBhIHJlZ3Jlc3Npb24gcGxhbmUgYW5kIHVzaW5nIHRoaXMgcGxhbmUgZm9yIHByZWRpY3Rpb25zLiBQcmVkaWN0aW9uIGlzIG9uZSBvZiB0aGUga2V5IHRhc2tzIG9mICdwcmVkaWN0aXZlIG1vZGVsaW5nLicgV2VsbCBkb25lIVwiKSIsImhpbnQiOiJSZW1lbWJlciB0aGF0IHlvdXIgcHJlZGljdGlvbiBpcyBpbiBsb2cgZG9sbGFycyBzbyB5b3UgbmVlZCB0byBleHBvbmVudGlhdGUgaXQgdG8gZ2V0IHRoZSByZXN1bHRzIGluIHRoZSBvcmlnaW5hbCBkb2xsYXIgdW5pdHMifQ==

3.1.3 Exercise. Interpreting coefficients as proportional changes

Assignment Text

In a previous exercise, you fit a MLR model using logface as the outcome variable and using education, numhh, and logincome as explanatory variables; the resulting fit is in the object Term_mlr. For this fit, the coefficient associated with education is 0.2064. We now wish to interpret this regression coefficient.

The typical interpretation of coefficients in a regression model is as a partial slope. That is, for the coefficient $b_1$ associated with $x_1$, we interpret $b_1$ to be amount that the expected outcome changes per unit change in $x_1$, holding the other explanatory variables fixed.

For the term life example, the units of the outcome are in logarithmic dollars. So, for small values of $b_1$, we can interpret this to be a proportional change in dollars.

Instructions

Determine least square fitted values for several selected values of education, holding other explantory variables fixed. For this part of the demonstration, we used their mean values.
Determine the proportional changes. Note the relation between these values from a discrete change approximation to the regression coefficient for education equal to 0.2064.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNUZXJtIDwtIHJlYWQuY3N2KFwiQ1NWRGF0YVxcXFx0ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvZWZjNjRiYzJkNzhjZjZiNDhhZDJjM2Y1ZTMxODAwY2I3NzNkZTI2MS90ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtMSA8LSBzdWJzZXQoVGVybSwgc3Vic2V0ID0gZmFjZSA+IDApXG5UZXJtMiA8LSBUZXJtMVssIGMoXCJlZHVjYXRpb25cIiwgXCJmYWNlXCIsIFwiaW5jb21lXCIsIFwibG9nZmFjZVwiLCBcImxvZ2luY29tZVwiLCBcIm51bWhoXCIpXVxuVGVybV9tbHIgPC0gbG0obG9nZmFjZSB+IGVkdWNhdGlvbiArIG51bWhoICsgbG9naW5jb21lLCBkYXRhID0gVGVybTIpIiwic2FtcGxlIjoiVGVybV9tbHIgPC0gbG0obG9nZmFjZSB+IGVkdWNhdGlvbiArIG51bWhoICsgbG9naW5jb21lLCBkYXRhID0gVGVybTIpXG5zdW1tYXJ5KFRlcm1fbWxyKSRjb2VmZmljaWVudHNbLDFdXG5cbiMgRGV0ZXJtaW5lIGxlYXN0IHNxdWFyZSBmaXR0ZWQgdmFsdWVzIGZvciBzZXZlcmFsIHNlbGVjdGVkIHZhbHVlcyBvZiBgZWR1Y2F0aW9uYCwgaG9sZGluZyBvdGhlciBleHBsYW50b3J5IHZhcmlhYmxlcyBmaXhlZC5cbmVkdWNfcHJlZGljdCA8LSBjKDE0LDE0LjEsMTQuMiwxNC4zKVxubmV3ZGF0YTEgPC0gZGF0YS5mcmFtZShsb2dpbmNvbWUgPSBtZWFuKFRlcm0yJGxvZ2luY29tZSksIGVkdWNhdGlvbiA9IGVkdWNfcHJlZGljdCwgbnVtaGggPSBtZWFuKFRlcm0yJG51bWhoKSlcbmxzZml0czEgPC0gcHJlZGljdChUZXJtX21sciwgbmV3ZGF0YTEpXG5sc2ZpdHMxXG5cbiMgRGV0ZXJtaW5lIHRoZSBwcm9wb3J0aW9uYWwgY2hhbmdlcy4gTm90ZSB0aGUgcmVsYXRpb24gYmV0d2VlbiB0aGVzZSB2YWx1ZXMgZnJvbSBhIGRpc2NyZXRlIGNoYW5nZSBhcHByb3hpbWF0aW9uIHRvIHRoZSByZWdyZXNzaW9uIGNvZWZmaWNpZW50IGZvciBgZWR1Y2F0aW9uYCBlcXVhbCB0byAwLjIwNjQuXG5sc2ZpdHMxWzI6NF0gLSBsc2ZpdHMxWzE6M11cbnBjaGFuZ2VfZml0czEgPC0gZXhwKGxzZml0czFbMjo0XSAtIGxzZml0czFbMTozXSlcbnBjaGFuZ2VfZml0czEiLCJzb2x1dGlvbiI6ImVkdWNfcHJlZGljdCA8LSBjKDE0LDE0LjEsMTQuMiwxNC4zKVxubmV3ZGF0YTEgPC0gZGF0YS5mcmFtZShsb2dpbmNvbWUgPSBtZWFuKFRlcm0yJGxvZ2luY29tZSksIGVkdWNhdGlvbiA9IGVkdWNfcHJlZGljdCwgbnVtaGggPSBtZWFuKFRlcm0yJG51bWhoKSlcbmxzZml0czEgPC0gcHJlZGljdChUZXJtX21sciwgbmV3ZGF0YTEpXG5sc2ZpdHMxXG5sc2ZpdHMxWzI6NF0gLSBsc2ZpdHMxWzE6M11cbnBjaGFuZ2VfZml0czEgPC0gZXhwKGxzZml0czFbMjo0XSAtIGxzZml0czFbMTozXSlcbnBjaGFuZ2VfZml0czEiLCJzY3QiOiJleCgpICU+JSBjaGVja19vYmplY3QoXCJlZHVjX3ByZWRpY3RcIiwgdW5kZWZpbmVkX21zZz1cIk1ha2Ugc3VyZSB0byBhc3NpZ24gdGhlIHZhbHVlcyBvZiBgZWR1Y2F0aW9uYCB0byBgZWR1Y19wcmVkaWN0YC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJUaGVzZSBudW1iZXJzIHNob3VsZCBiZSB0aGUgdmFsdWVzIGZyb20gMTQgdG8gMTQuMyBieSAuMSBpbmNyZW1lbnRzLiBcIilcbmV4KCkgJT4lIGNoZWNrX29iamVjdChcIm5ld2RhdGExXCIsdW5kZWZpbmVkX21zZz1cIk1ha2Ugc3VyZSB0byBjcmVhdGUgYSBkYXRhZnJhbWUgbmFtZWQgYG5ld2RhdGExYCBmb3IgcHJlZGljdGluZy4gXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiU2V0IGxvZyBpbmNvbWUgdG8gYmUgdGhlIG1lYW4gb2YgdGhlIGxvZ2luY29tZSBvZiBvdXIgZGF0YSwgZWR1Y2F0aW9uIGVxdWFsIHRvIGBlZHVjX3ByZWRpY3RgLCBhbmQgbnVtaGggZXF1YWwgdG8gdGhlIG1lYW4gb2YgbnVtaGguIFwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJwcmVkaWN0XCIsIG5vdF9jYWxsZWRfbXNnPVwiVXNlIGBwcmVkaWN0YCB0byBtYWtlIHByZWRpY3Rpb25zIGdpdmVuIG91ciBtb2RlbCBhbmQgZGF0YS5cIikgJT4lIHtcbiAgY2hlY2tfYXJnKC4sIFwib2JqZWN0XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIHNwZWNpZnkgdGhhdCB3ZSB3YW50IHRvIG1ha2UgcHJlZGljdGlvbnMgYmFzZWQgb24gYFRlcm1fbWxyYC5cIilcbiAgY2hlY2tfYXJnKC4sIFwibmV3ZGF0YVwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBzcGVjaWZ5IHRoYXQgd2Ugd291bGQgbGlrZSB0byB1c2UgdGhlIHZhbHVlcyBpbiBgbmV3ZGF0YTFgIGFzIHRoZSBkYXRhIGZvciBvdXIgcHJlZGljdGlvbnMuIFwiKVxufVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwibHNmaXRzMVwiLCB1bmRlZmluZWRfbXNnPVwiTWFrZSBzdXJlIHRvIGFzc2lnbiB0aGUgcHJlZGljdGVkIHZhbHVlcyB0byBgbHNmaXRzMWAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVXNlIGBwcmVkaWN0YCB0byBtYWtlIHByZWRpY3Rpb25zIGdpdmVuIG91ciBtb2RlbCBhbmQgZGF0YS5cIilcbmV4KCkgJT4lIGNoZWNrX29iamVjdChcInBjaGFuZ2VfZml0czFcIiwgdW5kZWZpbmVkX21zZz1cIk1ha2Ugc3VyZSB0byBhc3NpZ24gZXhwb25lbnRpYWwgb2YgdGhlIGRpZmZlcmVuY2VzIGJldHdlZW4gdGhlIGZpdCB2YWx1ZXMgdG8gYHBjaGFuZ2VfZml0czFgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoaXMgc2hvdWxkIGJlIGVxdWFsIHRvIHRoZSBleHBvbmVudGlhbCBvZiBlYWNoIGBsc2ZpdHMxYCBtaW51cyB0aGUgYGxzZml0czFgIHRoYXQgY2FtZSBkaXJlY3RseSBiZWZvcmUgaXQuXCIpXG5cbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwiZXhwXCIpICU+JSBjaGVja19hcmcoLiwgXCJ4XCIpICU+JSBjaGVja19lcXVhbCgpXG5cblxuc3VjY2Vzc19tc2coXCJDb25ncmF0dWxhdGlvbnMhIEZyb20gY2FsY3VsdXMsIHNtYWxsIGNoYW5nZXMgaW4gbG9nYXJpdGhtaWMgdmFsdWVzIGNhbiBiZSBpbnRlcnByZXRlZCBhcyBwcm9wb3J0aW9uYWwgY2hhbmdlcy4gVGhpcyBpcyB0aGUgcmVhc29uIGZvciB1c2luZyBuYXR1cmFsIGxvZ2FyaXRobXMuXCIpIiwiaGludCI6IlRvIGZpbmQgdGhlIHByb3BvcnRpb25hbCBjaGFuZ2VzLCB0YWtlIHRoZSAybmQtNHRoIG9ic2VydmF0aW9ucyBvZiA8Y29kZT5sc2ZpdHM8L2NvZGU+IGFuZCBzdWJ0cmFjdCB0aGUgMXN0LTNyZCBvYnNlcnZhdGlvbnMsIHRoZW4gZXhwb25lbnRpYXRlIHRoZSByZXN1bHRzLiJ9

3.1.4 Exercise. Interpreting coefficients as elasticities

Assignment Text

In a previous exercise, you fit a MLR model using logface as the outcome variable and using education, numhh, and logincome as explanatory variables; the resulting fit is in the object Term_mlr. From this fit, the coefficient associated with logincome is 0.4935. We now wish to interpret this regression coefficient.

The typical interpretation of coefficients in a regression model is as a partial slope. When both $x_1$ and $y$ are in logarithmic units, then we can interpret $b_1$ to be ratio of two percentage changes, known as an elasticity in economics. Mathematically, we summarize this as \[ \frac{\partial \ln y}{\partial \ln x} = \left(\frac{\partial y}{y}\right) ~/ ~\left(\frac{\partial x}{x}\right) . \]

Instructions

For several selected values of logincome, determine the corresponding proportional changes.
Determine least square fitted values for several selected values of logincome, holding other explantory variables fixed.
Determine the corresponding proportional changes for the fitted values.
Calculate the ratio of proportional changes of fitted values to those for income. Note the relation between these values (from a discrete change approximation) to the regression coefficient for logincome equal to 0.4935.

Hint. When you calculate the ratio of proportional changes of fitted values to those for income, note the relation between these values (from a discrete change approximation) to the regression coefficient for logincome equal to 0.4935.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNUZXJtIDwtIHJlYWQuY3N2KFwiQ1NWRGF0YVxcXFx0ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvZWZjNjRiYzJkNzhjZjZiNDhhZDJjM2Y1ZTMxODAwY2I3NzNkZTI2MS90ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtMSA8LSBzdWJzZXQoVGVybSwgc3Vic2V0ID0gZmFjZSA+IDApXG5UZXJtMiA8LSBUZXJtMVssIGMoXCJlZHVjYXRpb25cIiwgXCJmYWNlXCIsIFwiaW5jb21lXCIsIFwibG9nZmFjZVwiLCBcImxvZ2luY29tZVwiLCBcIm51bWhoXCIpXVxuVGVybV9tbHIgPC0gbG0obG9nZmFjZSB+IGVkdWNhdGlvbiArIG51bWhoICsgbG9naW5jb21lLCBkYXRhID0gVGVybTIpIiwic2FtcGxlIjoiVGVybV9tbHIgPC0gbG0obG9nZmFjZSB+IGVkdWNhdGlvbiArIG51bWhoICsgbG9naW5jb21lLCBkYXRhID0gVGVybTIpXG5zdW1tYXJ5KFRlcm1fbWxyKSRjb2VmZmljaWVudHNbLDFdXG4jIEZvciBzZXZlcmFsIHNlbGVjdGVkIHZhbHVlcyBvZiBgbG9naW5jb21lYCwgZGV0ZXJtaW5lIHRoZSBjb3JyZXNwb25kaW5nIHByb3BvcnRpb25hbCBjaGFuZ2VzLlxubG9naW5jb21lX3ByZWQgPC0gYygxMSwxMS4xLDExLjIsMTEuMylcbnBjaGFuZ2VfaW5jb21lIDwtIDEwMCooZXhwKGxvZ2luY29tZV9wcmVkWzI6NF0pL2V4cChsb2dpbmNvbWVfcHJlZFsxOjNdKS0xKVxucGNoYW5nZV9pbmNvbWVcblxuIyBEZXRlcm1pbmUgbGVhc3Qgc3F1YXJlIGZpdHRlZCB2YWx1ZXMgZm9yIHNldmVyYWwgc2VsZWN0ZWQgdmFsdWVzIG9mIGBsb2dpbmNvbWVgLCBob2xkaW5nIG90aGVyIGV4cGxhbnRvcnkgdmFyaWFibGVzIGZpeGVkLlxubmV3ZGF0YTIgPC0gZGF0YS5mcmFtZShsb2dpbmNvbWUgPSBsb2dpbmNvbWVfcHJlZCwgZWR1Y2F0aW9uID0gbWVhbihUZXJtMiRlZHVjYXRpb24pLCBudW1oaCA9IG1lYW4oVGVybTIkbnVtaGgpKVxubHNmaXRzMiA8LSBwcmVkaWN0KFRlcm1fbWxyLCBuZXdkYXRhMilcblxuIyBEZXRlcm1pbmUgdGhlIGNvcnJlc3BvbmRpbmcgcHJvcG9ydGlvbmFsIGNoYW5nZXMgZm9yIHRoZSBmaXR0ZWQgdmFsdWVzLiBcbnBjaGFuZ2VfZml0czIgPC0gMTAwKihleHAobHNmaXRzMlsyOjRdKS9leHAobHNmaXRzMlsxOjNdKS0xKVxucGNoYW5nZV9maXRzMlxuXG4jIENhbGN1bGF0ZSB0aGUgcmF0aW8gb2YgcHJvcG9ydGlvbmFsIGNoYW5nZXMgb2YgZml0dGVkIHZhbHVlcyB0byB0aG9zZSBmb3IgaW5jb21lLlxucGNoYW5nZV9maXRzMi9wY2hhbmdlX2luY29tZSIsInNvbHV0aW9uIjoibG9naW5jb21lX3ByZWQgPC0gYygxMSwxMS4xLDExLjIsMTEuMylcbnBjaGFuZ2VfaW5jb21lIDwtIDEwMCooZXhwKGxvZ2luY29tZV9wcmVkWzI6NF0pL2V4cChsb2dpbmNvbWVfcHJlZFsxOjNdKS0xKVxucGNoYW5nZV9pbmNvbWVcbm5ld2RhdGEyIDwtIGRhdGEuZnJhbWUobG9naW5jb21lID0gbG9naW5jb21lX3ByZWQsIGVkdWNhdGlvbiA9IG1lYW4oVGVybTIkZWR1Y2F0aW9uKSwgbnVtaGggPSBtZWFuKFRlcm0yJG51bWhoKSlcbmxzZml0czIgPC0gcHJlZGljdChUZXJtX21sciwgbmV3ZGF0YTIpXG5wY2hhbmdlX2ZpdHMyIDwtIDEwMCooZXhwKGxzZml0czJbMjo0XSkvZXhwKGxzZml0czJbMTozXSktMSlcbnBjaGFuZ2VfZml0czJcbnBjaGFuZ2VfZml0czIvcGNoYW5nZV9pbmNvbWUiLCJzY3QiOiJleCgpICU+JSBjaGVja19vYmplY3QoXCJsb2dpbmNvbWVfcHJlZFwiLCB1bmRlZmluZWRfbXNnPVwiQXNzaWduIHRoZSBzdHJpbmcgb2YgdmFsdWVzIHRvIGBsb2dpbmNvbWVfcHJlZGAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhlIHZhbHVlcyBzaG91bGQgYmUgYDExYCwgYDExLjFgLCBgMTEuMmAsIGFuZCBgMTEuM2AuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJwY2hhbmdlX2luY29tZVwiLCB1bmRlZmluZWRfbXNnPVwiYXNzaWduIHRoZSB2YWx1ZXMgb2YgdGhlIHBlcmNlbnRhZ2UgY2hhbmdlIGluIGluY29tZS4gXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiaXQgc2hvdWxkIGJlIGVxdWFsIHRvIHRoZSBmb2xsb3dpbmc6IGAxMDAqKGV4cChsb2dpbmNvbWVfcHJlZFsyOjRdKS9leHAobG9naW5jb21lX3ByZWRbMTozXSktMWAuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJuZXdkYXRhMlwiLCB1bmRlZmluZWRfbXNnPVwiY3JlYXRlIHNvbWUgbmV3IGRhdGEsIGFuZCBuYW1lIGl0IHRvIGBuZXdkYXRhMmAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhpcyBuZXcgZGF0YSBzaG91bGQgaGF2ZSBgbG9naW5jb21lYCBlcXVhbCB0byBgbG9naW5jb21lX3ByZWRgLCBgZWR1Y2F0aW9uYCBlcXVhbCB0byB0aGUgbWVhbiBvZiBgZWR1Y2F0aW9uYCwgYW5kIGBudW1oaGAgZXF1YWwgdG8gdGhlIG1lYW4gb2YgYG51bWhoYC5cIilcbmV4KCkgJT4lIGNoZWNrX29iamVjdChcImxzZml0czJcIiwgdW5kZWZpbmVkX21zZz1cIlNldCB0aGUgcHJlZGljdGVkIHZhbHVlcyB0byBiZSBzdG9yZWQgaW4gYGxzZml0czJgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cInlvdSBzaG91bGQgcnVuIHByZWRpY3Qgb24gYFRlcm1fbWxyYCBhbmQgYG5ld2RhdGEyYC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwicHJlZGljdFwiLCBub3RfY2FsbGVkX21zZz1cIlVzZSBgcHJlZGljdGAgdG8gY3JlYXRlIHRoZSBwcmVkaWN0ZWQgdmFsdWVzLiBcIikgJT4lIHtcbiAgY2hlY2tfYXJnKC4sIFwib2JqZWN0XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhlIG1vZGVsIHRoYXQgd2Ugd2FudCB0byB1c2UgaXMgYFRlcm1fbWxyYC5cIilcbiAgY2hlY2tfYXJnKC4sIFwibmV3ZGF0YVwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoZSBkYXRhIHdlIHdhbnQgdG8gdXNlIHRvIGNyZWF0ZSBwcmVkaWN0aW9ucyBpcyBmb3VuZCBpbiBgbmV3ZGF0YTJgLlwiKVxufVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwicGNoYW5nZV9maXRzMlwiLCB1bmRlZmluZWRfbXNnPVwibm93IGZpbmQgdGhlIHBlcmNlbnRhZ2UgY2hhbmdlIGluIGVhY2ggb2YgdGhlIGZpdHMsIGFuZCBzdG9yZSB0aGVtIGluIGBwY2hhbmdlX2ZpdHMyYC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJEbyB0aGUgZXhhY3Qgc2FtZSB0aGluZyB5b3UgZGlkIGZvciBgcGNoYW5nZV9pbmNvbWVgLCBleGNlcHQgdXNlIHRoZSBmaXRzIGluc3RlYWQgb2YgdGhlIHByZWRpY3Rpb25zLiBcIilcbnN1Y2Nlc3NfbXNnKFwiQ29uZ3JhdHVsYXRpb25zISBXaGVuIGJvdGggJHhfMSQgYW5kICR5JCBhcmUgaW4gbG9nYXJpdGhtaWMgdW5pdHMsIHRoZW4gd2UgY2FuIGludGVycHJldCAkYl8xJCB0byBiZSByYXRpbyBvZiB0d28gcGVyY2VudGFnZSBjaGFuZ2VzLCBrbm93biBhcyBhbiAqZWxhc3RpY2l0eSogaW4gZWNvbm9taWNzLlwiKSIsImhpbnQiOiJXaGVuIHlvdSBjYWxjdWxhdGUgdGhlIHJhdGlvIG9mIHByb3BvcnRpb25hbCBjaGFuZ2VzIG9mIGZpdHRlZCB2YWx1ZXMgdG8gdGhvc2UgZm9yIGluY29tZSwgbm90ZSB0aGUgcmVsYXRpb24gYmV0d2VlbiB0aGVzZSB2YWx1ZXMgKGZyb20gYSBkaXNjcmV0ZSBjaGFuZ2UgYXBwcm94aW1hdGlvbikgdG8gdGhlIHJlZ3Jlc3Npb24gY29lZmZpY2llbnQgZm9yIDxjb2RlPmxvZ2luY29tZTwvY29kZT4gZXF1YWwgdG8gMC40OTM1LiJ9

3.2 Statistical inference and multiple linear regresson

In this section, you learn how to:

Explain mean square error and residual standard error in terms of degrees of freedom
Develop an ANOVA table and use it to derive the coefficient of determination
Calculate and interpret the coefficient of determination adjusted for degrees of freedom
Conduct a test of a regression coefficient
Summarize regression coefficients using point and interval estimators

3.2.1 Video

Video Overhead Details

A Details. Goodness of fit

Summarize

deviations
$s^2$
$R^2$
$R_a^2$
ANOVA table

B Details. Goodness of fit and term life

Term_mlr <- lm(logface ~ education + numhh + logincome, data = Term2)
summary(Term_mlr)
anova(Term_mlr)


Call:
lm(formula = logface ~ education + numhh + logincome, data = Term2)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.7420 -0.8681  0.0549  0.9093  4.7187 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.58408    0.84643   3.053  0.00249 ** 
education    0.20641    0.03883   5.316 2.22e-07 ***
numhh        0.30605    0.06333   4.833 2.26e-06 ***
logincome    0.49353    0.07754   6.365 8.32e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.525 on 271 degrees of freedom
Multiple R-squared:  0.3425,    Adjusted R-squared:  0.3353 
F-statistic: 47.07 on 3 and 271 DF,  p-value: < 2.2e-16

Analysis of Variance Table

Response: logface
           Df Sum Sq Mean Sq F value    Pr(>F)    
education   1 140.55 140.549  60.417 1.601e-13 ***
numhh       1  93.68  93.681  40.270 9.251e-10 ***
logincome   1  94.24  94.238  40.510 8.316e-10 ***
Residuals 271 630.43   2.326                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

C Details. Statistical inference

hypothesis testing of a regression coefficient
confidence intervals

D Details. Statistical inference and term life

Term_mlr <- lm(logface ~ education + numhh + logincome, data = Term2)
model_sum <- summary(Term_mlr)
model_sum$coefficients

round(confint(Term_mlr, level = .95), digits = 3)

round(confint(Term_mlr, level = .95), digits = 3)

             Estimate Std. Error  t value     Pr(>|t|)
(Intercept) 2.5840786 0.84642972 3.052916 2.491588e-03
education   0.2064139 0.03883186 5.315581 2.223619e-07
numhh       0.3060455 0.06332511 4.832926 2.255708e-06
logincome   0.4935323 0.07754198 6.364711 8.316097e-10
            2.5 % 97.5 %
(Intercept) 0.918  4.250
education   0.130  0.283
numhh       0.181  0.431
logincome   0.341  0.646
            2.5 % 97.5 %
(Intercept) 0.918  4.250
education   0.130  0.283
numhh       0.181  0.431
logincome   0.341  0.646

3.2.2 Exercise. Statistical inference and term life

Assignment Text

In later chapters, we will learn how to specify a model using diagnostics techniques; these techniques were used to specify face in log dollars for the outcome and similarly income in log dollars as an explanatory variable. Just to see how things work, in this exercise we will create new variables face and income that are in the original units and run a regression with these. We have already seen that rescaling by constants do not affect relationships but can be helpful with interpretations, so we define both face and income to be in thousands of dollars. A prior video introduced the term life dataframe Term2.

Instructions

Create Term2$face by exponentiating logface and dividing by 1000. For convenience, we are storing this variable in the data set Term2. Use the same process to create Term2$income.
Run a regression using face as the outcome variable and education, numhh, and income as explanatory variables.
Summarize this model and identify the residual standard error ($s$) as well as the coefficient of determination ($R^2$) and the version adjusted for degrees of freedom ($R_a^2$).

3.3 Binary variables

In this section, you learn how to:

Interpret regression coefficients associated with binary variables
Use binary variables and interaction terms to create regression models that are nonlinear in the covariates

3.3.1 Video

Video Overhead Details

A Details. Binary variables

We can define a new variable \[ single= \left\{ \begin{array}{ll} 0 & \text{for other respondents} \\ 1 & \text{for single respondents} \end{array} \right. \]
The variable single is said to be an indicator, or dummy, variable.
To interpret coefficients, we now consider the regression function

\[ \text{E }logface = \beta_0 + \beta_1 logincome + \beta_2 single \] - This can be expressed as two lines \[ \text{E }logface = \left\{ \begin{array}{ll} \beta_0 + \beta_1 logincome & \textrm{for other respondents} \\ \beta_0 + \beta_2 + \beta_1 logincome & \textrm{for single respondents} \end{array} \right. . \] - The least squares method of calculating the estimators, and the resulting theoretical properties, are the still valid when using binary variables.

B Details. Visualize effect of binary variables

C Details. R script for visualization

Term4 <- Term1[,c("numhh", "education", "logincome", "logface", "marstat")]
Term4$marstat <- as.factor(Term4$marstat)
table(Term4$marstat)
Term4$single <- 1*(Term4$marstat == 0)
model_single <- lm(logface ~ logincome + single, data = Term4)
summary(model_single)

plot(Term4$logincome,Term4$logface,xlab="logarithmic income", ylab="log face",
    pch= 1+16*Term4$single, col = c("red", "black", "black")[Term4$marstat])
Ey1 <- model_single$coefficients[1]+model_single$coefficients[2]*Term4$logincome
Ey2 <- Ey1 + model_single$coefficients[3]
lines(Term4$logincome, Ey1)
lines(Term4$logincome, Ey2, col="red")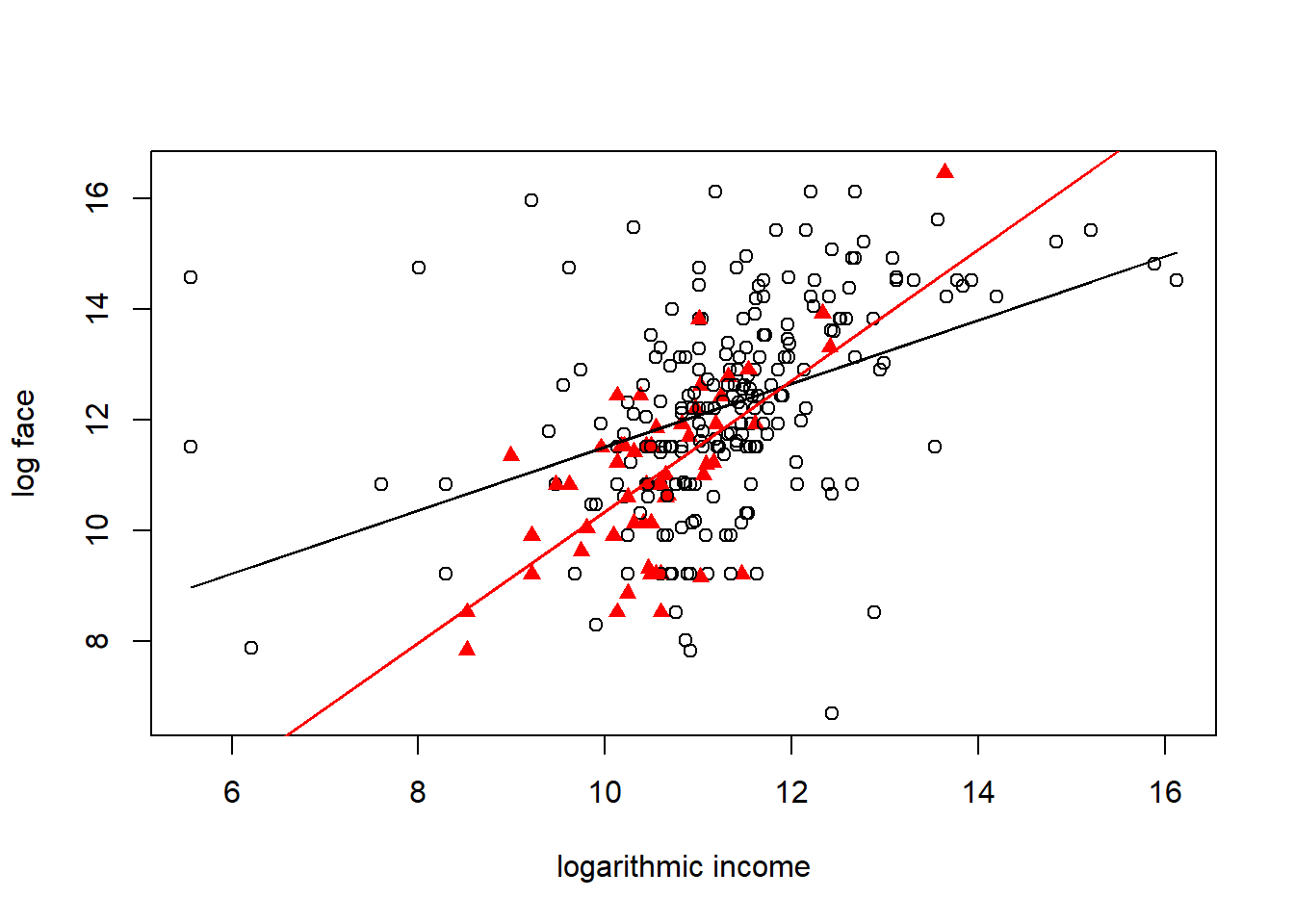


  0   1   2 
 57 208  10 

Call:
lm(formula = logface ~ logincome + single, data = Term4)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.2828 -0.8785  0.0364  0.9227  5.9573 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  5.09007    0.88643   5.742 2.49e-08 ***
logincome    0.63378    0.07776   8.151 1.33e-14 ***
single      -0.80006    0.24796  -3.227  0.00141 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.615 on 272 degrees of freedom
Multiple R-squared:  0.2605,    Adjusted R-squared:  0.255 
F-statistic:  47.9 on 2 and 272 DF,  p-value: < 2.2e-16

D Details. Interaction Terms

Linear regression models are defined in terms of linear combinations of explanatory varibles but we can expand their scope through nonlinear transformations
- One type of nonlinear transform is the product of two varibles that is used to create what is known as an interaction variable
To interpret coefficients, we now consider the regression function

\[ \text{E }logface = \beta_0 + \beta_1 logincome + \beta_2 single + \beta_3 single*logincome \] - This can be expressed as two lines with different slopes \[ \text{E }logface = \left\{ \begin{array}{ll} \beta_0 + \beta_1 logincome & \textrm{for other respondents} \\ \beta_0 + \beta_2 + (\beta_1 + \beta_3) logincome & \textrm{for single respondents} \end{array} \right. . \]

E Details. Visualizing binary variables with interactions terms

Term4 <- Term1[,c("numhh", "education", "logincome", "logface", "marstat")]
Term4$marstat <- as.factor(Term4$marstat)
table(Term4$marstat)
Term4$single <- 1*(Term4$marstat == 0)
model_single_inter <- lm(logface ~ logincome + single + single*logincome, data = Term4)
summary(model_single_inter)

plot(Term4$logincome,Term4$logface,xlab="logarithmic income", ylab="log face",
    pch= 1+16*Term4$single, col = c("red", "black", "black")[Term4$marstat])
Ey1 <- model_single_inter$coefficients[1]+model_single_inter$coefficients[2]*Term4$logincome
Ey2 <- Ey1 + model_single_inter$coefficients[3]+model_single_inter$coefficients[4]*Term4$logincome
lines(Term4$logincome, Ey1)
lines(Term4$logincome, Ey2, col="red")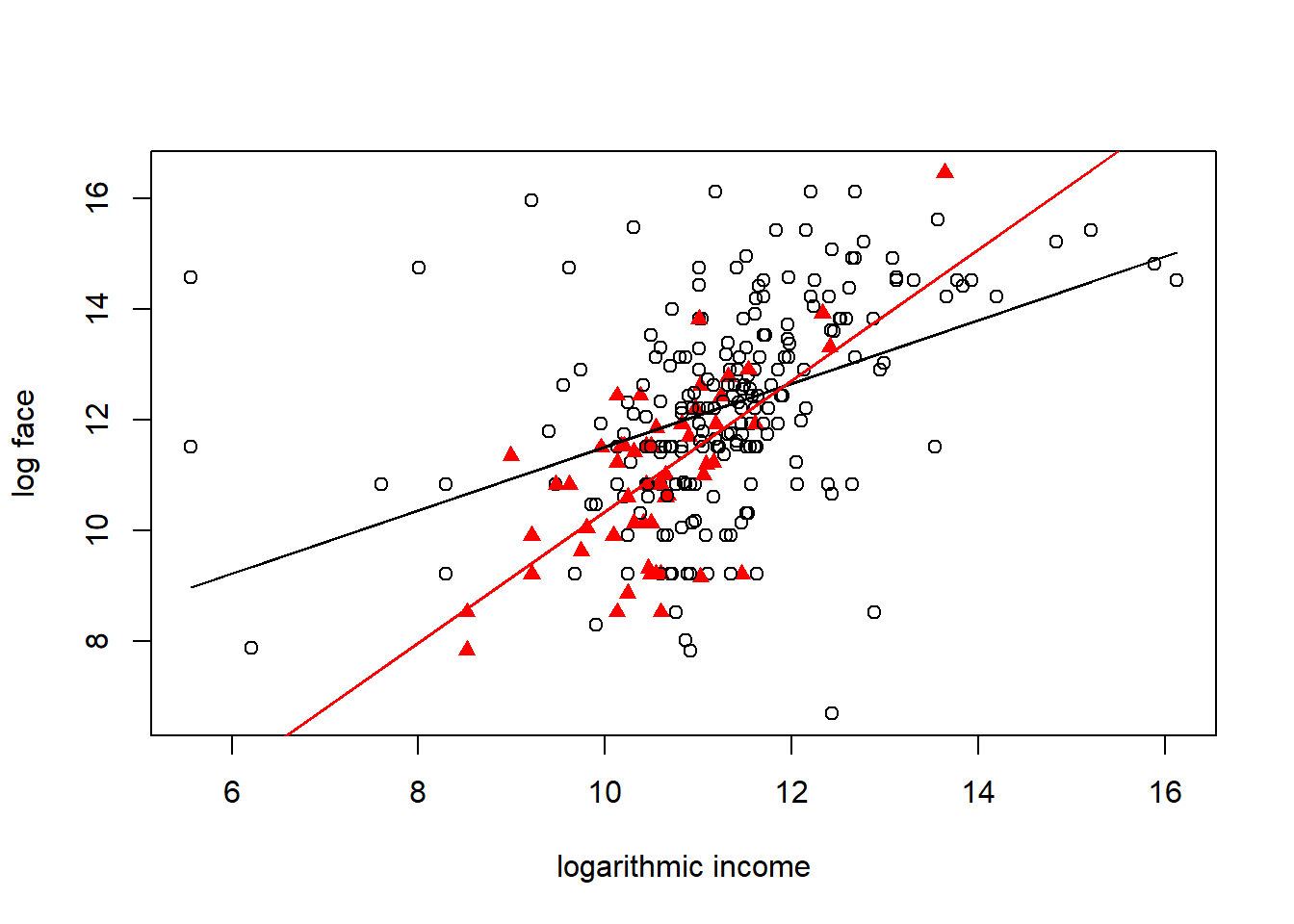


  0   1   2 
 57 208  10 

Call:
lm(formula = logface ~ logincome + single + single * logincome, 
    data = Term4)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.2149 -0.8287  0.0696  0.9308  5.6070 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)       5.77902    0.92550   6.244 1.64e-09 ***
logincome         0.57288    0.08124   7.051 1.47e-11 ***
single           -7.29211    2.74216  -2.659   0.0083 ** 
logincome:single  0.61244    0.25764   2.377   0.0181 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.601 on 271 degrees of freedom
Multiple R-squared:  0.2756,    Adjusted R-squared:  0.2676 
F-statistic: 34.36 on 3 and 271 DF,  p-value: < 2.2e-16

3.3.2 Exercise. Binary variables and term life

Assignment Text

In the prior video, we saw how the variable single can be used with logarithmic income to explain logarithmic face amounts of term life insurance that people purchase. The coefficient associated with this variable turns out to be negative which is intuitively appealing; if an individual is single, then that person may not have the strong need to purchase financial security for others in the event of unexpected death.

In this exercise, we will extend this by incorporating single into our larger regression model that contains other explanatory varibles, logincome, education and numhh. The data have been pre-loaded into the dataframe Term4.

Instructions

Calculate a table of correlation coefficients to examine pairwise linear relationships among the variables numhh, education, logincome, single, and logface.
Fit a MLR model of logface using explanatory variables numhh, education, logincome, and single. Examine the residual standard deviation $s$, the coefficient of determination $R^2$, and the adjusted version $R_a^2$. Also note the statistical significance of the coefficient associated with single.
Repeat the MLR model fit while adding the interaction term single*logincome.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNUZXJtIDwtIHJlYWQuY3N2KFwiQ1NWRGF0YVxcXFx0ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvZWZjNjRiYzJkNzhjZjZiNDhhZDJjM2Y1ZTMxODAwY2I3NzNkZTI2MS90ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtMSA8LSBzdWJzZXQoVGVybSwgc3Vic2V0ID0gZmFjZSA+IDApXG5UZXJtNCA8LSBUZXJtMVssYyhcIm51bWhoXCIsIFwiZWR1Y2F0aW9uXCIsIFwibG9naW5jb21lXCIsIFwibWFyc3RhdFwiLCBcImxvZ2ZhY2VcIildXG5UZXJtNCRzaW5nbGUgPC0gMSooVGVybTQkbWFyc3RhdCA9PSAwKSIsInNhbXBsZSI6IiMgQ2FsY3VsYXRlIGEgdGFibGUgb2YgY29ycmVsYXRpb24gY29lZmZpY2llbnRzXG5yb3VuZChfX18oVGVybTRbLGMoXCJudW1oaFwiLCBcImVkdWNhdGlvblwiLCBcImxvZ2luY29tZVwiLCBcInNpbmdsZVwiLCBcImxvZ2ZhY2VcIildKSwgZGlnaXRzID0gMylcblxuIyBGaXQgYSBNTFIgbW9kZWwgb2YgYGxvZ2ZhY2VgIHVzaW5nIGV4cGxhbmF0b3J5IHZhcmlhYmxlcyBgbnVtaGhgLCBgZWR1Y2F0aW9uYCwgYGxvZ2luY29tZWAsIGFuZCBgc2luZ2xlYC5cblRlcm1fbWxyMyA8LSBsbShsb2dmYWNlIH4gZWR1Y2F0aW9uICsgbnVtaGggKyBsb2dpbmNvbWUgKyBzaW5nbGUsIGRhdGEgPSBUZXJtNClcbnN1bW1hcnkoVGVybV9tbHIzKVxuXG4jIFJlcGVhdCB0aGUgTUxSIG1vZGVsIGZpdCB3aGlsZSBhZGRpbmcgdGhlIGludGVyYWN0aW9uIHRlcm0gIGBzaW5nbGUqbG9naW5jb21lYC5cblRlcm1fbWxyNCA8LSBsbShsb2dmYWNlIH4gZWR1Y2F0aW9uICsgbnVtaGggKyBsb2dpbmNvbWUgKyBzaW5nbGUgKyBzaW5nbGUqbG9naW5jb21lLCBkYXRhID0gVGVybTQpXG5zdW1tYXJ5KFRlcm1fbWxyNCkiLCJzb2x1dGlvbiI6InJvdW5kKGNvcihUZXJtNFssYyhcIm51bWhoXCIsIFwiZWR1Y2F0aW9uXCIsIFwibG9naW5jb21lXCIsIFwic2luZ2xlXCIsIFwibG9nZmFjZVwiKV0pLCBkaWdpdHMgPSAzKVxuVGVybV9tbHIzIDwtIGxtKGxvZ2ZhY2UgfiBlZHVjYXRpb24gKyBudW1oaCArIGxvZ2luY29tZSArIHNpbmdsZSwgZGF0YSA9IFRlcm00KVxuc3VtbWFyeShUZXJtX21scjMpXG5UZXJtX21scjQgPC0gbG0obG9nZmFjZSB+IGVkdWNhdGlvbiArIG51bWhoICsgbG9naW5jb21lICsgc2luZ2xlICsgc2luZ2xlKmxvZ2luY29tZSwgZGF0YSA9IFRlcm00KVxuc3VtbWFyeShUZXJtX21scjQpIiwic2N0IjoiZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJyb3VuZFwiLCBub3RfY2FsbGVkX21zZz1cIlVzZSBgcm91bmRgIG9uIHRoZSBjb3JyZWxhdGlvbiBjb2VmZmljaWVudHMgZm91bmQgdXNpbmcgYGNvcmAgdG8gMyBkaWdpdHMuXCIpICU+JSBjaGVja19yZXN1bHQoKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlVzZSBgY29yYCB0byBmaW5kIHRoZSBjb3JyZWxhdGlvbnMsIGFuZCB0aGVuIHJvdW5kIHRoZW0gdG8gMyBkaWdpdHMuIFwiKVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwiVGVybV9tbHIzXCIsIHVuZGVmaW5lZF9tc2c9XCJVc2UgYGxtYCB0byBjcmVhdGUgYSBsaW5lYXIgbW9kZWwgbmFtZWQgYFRlcm1fbWxyM2AuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiWW91IGxpbmVhciBtb2RlbCBzaG91bGQgbW9kZWwgYGxvZ2ZhY2VgIGJhc2VkIG9uIGBlZHVjYXRpb25gLCBgbnVtaGhgLCBgbG9naW5jb21lYCwgYW5kIGBzaW5nbGVgIGZyb20gdGhlIGRhdGEgaW4gYFRlcm00YC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwic3VtbWFyeVwiLGluZGV4PTEsbm90X2NhbGxlZF9tc2c9XCJVc2UgYHN1bW1hcnlgIHRvIHZpZXcgYSBzdW1tYXJ5IG9mIGBUZXJtX21scjNgLlwiKSAlPiUgY2hlY2tfcmVzdWx0KCkgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc3BlY2lmeSB0aGF0IHdlIHdhbnQgYSBzdW1tYXJ5IG9mIGBUZXJtX21scjNgLlwiKVxuIGV4KCkgJT4lIGNoZWNrX29iamVjdChcIlRlcm1fbWxyNFwiLCB1bmRlZmluZWRfbXNnPVwiVXNlIGBsbWAgdG8gY3JlYXRlIGEgbGluZWFyIG1vZGVsIG5hbWVkIGBUZXJtX21scjRgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIllvdSBsaW5lYXIgbW9kZWwgc2hvdWxkIG1vZGVsIGBsb2dmYWNlYCBiYXNlZCBvbiBgZWR1Y2F0aW9uYCwgYG51bWhoYCwgYGxvZ2luY29tZWAsIGFuZCB0aGUgcHJvZHVjdCBvZiBgc2luZ2xlYCBhbmQgYGxvZ2luY29tZWAgZnJvbSB0aGUgZGF0YSBpbiBgVGVybTRgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsaW5kZXg9Mixub3RfY2FsbGVkX21zZz1cIlVzZSBgc3VtbWFyeWAgdG8gdmlldyBhIHN1bW1hcnkgb2YgYFRlcm1fbWxyNGAuXCIpICU+JSBjaGVja19yZXN1bHQoKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBzcGVjaWZ5IHRoYXQgd2Ugd2FudCBhIHN1bW1hcnkgb2YgYFRlcm1fbWxyNGAuXCIpXG5zdWNjZXNzX21zZyhcIkNvbmdyYXR1bGF0aW9ucyEgRnJvbSBhIGNvcnJlbGF0aW9uIHRhYmxlLCB5b3Ugc2F3IHRoYXQgdGhlcmUgYXJlIHJlbGF0aW9uc2hpcHMgd2l0aCBhbW9uZyBleHBsYW5hdG9yeSB2YXJpYWJsZXMgYW5kIHNvIGl0IGlzIG5vdCBjbGVhciB3aGV0aGVyIGFkZGluZyBgc2luZ2xlYCB0byB0aGUgbW9kZWwgd291bGQgYmUgaGVscGZ1bC4gWW91IGV4cGxvcmVkIHRoaXMgYnkgZmlyc3QgZml0dGluZyBhIG1vZGVsIGJ5IGp1c3QgYWRkaW5nIHRoZSBiaW5hcnkgdmFyaWFibGUgc2luZ2xlLCBleGFtaW5lZCBzdW1tYXJ5IHN0YXRpc3RpY3MsIGFuZCBjaGVja2VkIHRoZSBzaWduaWZpY2FuY2Ugb2YgdGhlIHZhcmlhYmxlLiBUaGVuLCB5b3UgZXhwbG9yZWQgdGhlIHV0aWxpdHkgb2YgdGhlIGludGVyYWN0aW9uIG9mIGBzaW5nbGVgIHdpdGggbG9nYXJpdGhtaWMgaW5jb21lLiBXZWxsIGRvbmUhXCIpIiwiaGludCI6IlRvIGdldCBhIHRhYmxlIG9mIGNvcnJlbGF0aW9ucywgdGhlIDxjb2RlPmNvcigpPC9jb2RlPiBmdW5jdGlvbiBjYW4gYmUgdXNlZC5cbkFmdGVyIHRoYXQsIGEgY29tYmluYXRpb24gb2YgPGNvZGU+bG0oKTwvY29kZT4gYW5kIDxjb2RlPnN1bW1hcnkoKTwvY29kZT4gY2FuIGJlIHVzZWQgdG8gYWNoaWV2ZSB0aGUgZGVzaXJlZCByZXN1bHRzIn0=

3.4 Categorical variables

In this section, you learn how to:

Represent categorical variables using a set of binary variables
Interpret the regression coefficients associated with categorical variables
Describe the effect of the reference level choice on the model fit

3.4.1 Video

Video Overhead Details

A Details. Categorical variables

Categorical variables provide labels for observations to denote membership in distinct groups, or categories.
A binary variable is a special case of a categorical variable.
- To illustrate, a binary variable may tell us whether or not someone has health insurance.
- A categorical variable could tell us whether someone has (i) private individual health insurance, (ii) private group insurance, (iii) public insurance or (iv) no health insurance.
For categorical variables, there may or may not be an ordering of the groups.
- For health insurance, it is difficult to say which is ‘larger’, private individual versus public health insurance (such as Medicare).
- However, for education, we may group individuals from a dataset into ‘low’, ‘intermediate’ and ‘high’ years of education.
Factor is another term used for a (unordered) categorical explanatory variable.

B Details. Term life example

We studied y = logface, the amount that the company will pay in the event of the death of the named insured (in logarithmic dollars), focusing on the explanatory variables logincome, education, and numhh.
We now supplement this by including the categorical variable, marstat, that is the marital status of the survey respondent. This may be:
- 1, for married
- 2, for living with partner
- 0, for other (SCF actually breaks this category into separated, divorced, widowed, never married and inapplicable, for persons age 17 or less or no further persons)

C Details. Term life boxplots

# Pre-exercise code
#Term <- read.csv("CSVData\\term_life.csv", header = TRUE)
Term <- read.csv("https://assets.datacamp.com/production/repositories/2610/datasets/efc64bc2d78cf6b48ad2c3f5e31800cb773de261/term_life.csv", header = TRUE)
Term1 <- subset(Term, subset = face > 0)
Term4 <- Term1[,c("numhh", "education", "logincome", "marstat", "logface")]
Term4$single <- 1*(Term4$marstat == 0)
Term4$marstat<- as.factor(Term4$marstat)
boxplot(logface ~ marstat, ylab = "log face", xlab = "Marital Status", data = Term4)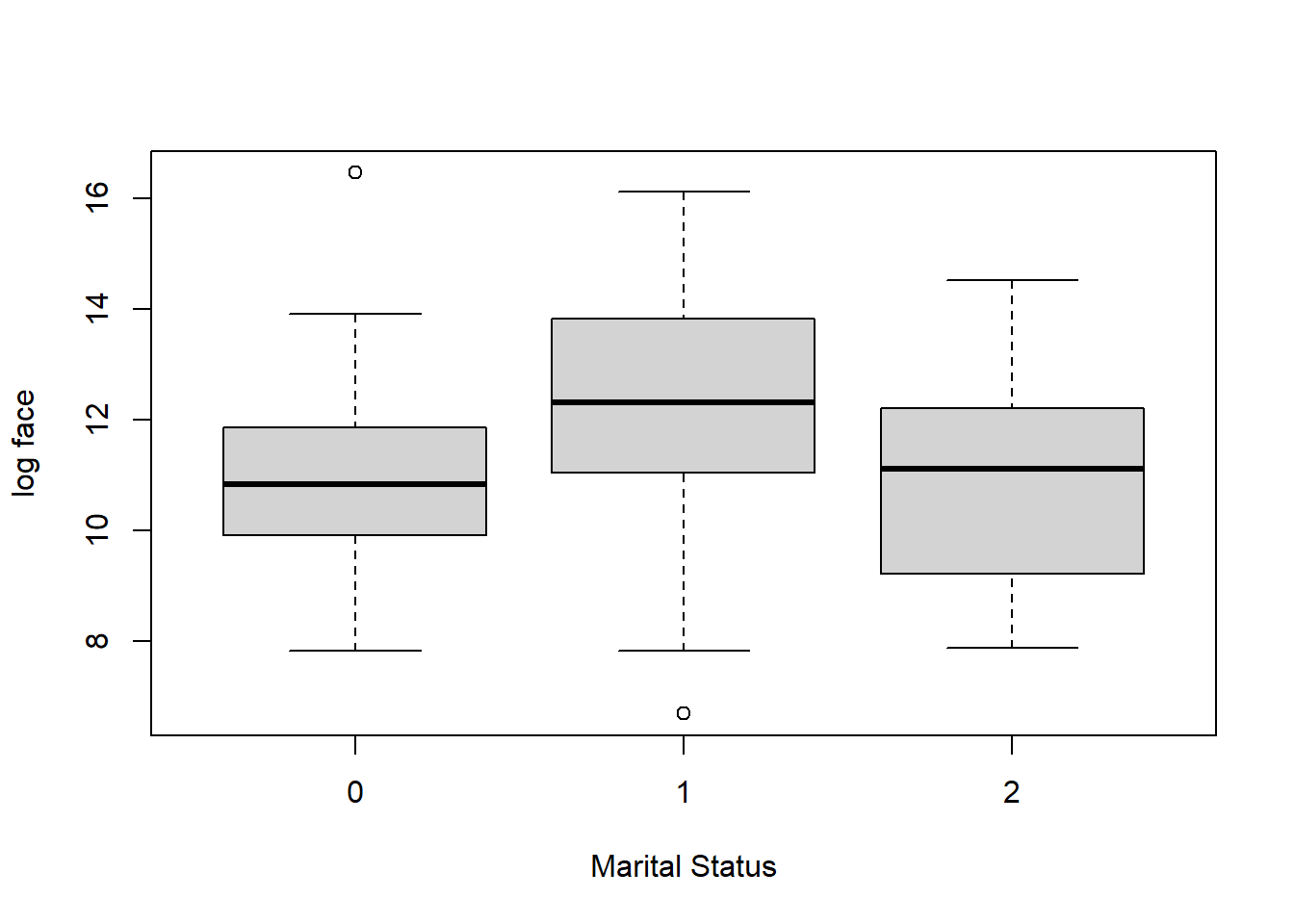

table(Term4$marstat)
#  SUMMARY BY LEVEL OF MARSTAT
#library(Rcmdr)
#numSummary(Term4[, "logface"], groups = Term4$marstat, statistics = c("mean", "sd"))
#numSummary(Term4[, "logface"], statistics = c("mean", "sd"))


  0   1   2 
 57 208  10

D Details. Regression with a categorical variable

Term4$marstat <- as.factor(Term4$marstat)
Term4$marstat <- relevel(Term4$marstat, ref = "2")
summary(lm(logface ~ logincome+education+numhh+marstat, data = Term4))


Call:
lm(formula = logface ~ logincome + education + numhh + marstat, 
    data = Term4)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.8875 -0.8505  0.1124  0.8468  4.5173 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.60536    0.95218   2.736 0.006629 ** 
logincome    0.45151    0.07872   5.736 2.61e-08 ***
education    0.20467    0.03862   5.299 2.42e-07 ***
numhh        0.24770    0.06940   3.569 0.000424 ***
marstat0     0.23234    0.53283   0.436 0.663155    
marstat1     0.78941    0.49532   1.594 0.112169    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.513 on 269 degrees of freedom
Multiple R-squared:  0.358, Adjusted R-squared:  0.3461 
F-statistic:    30 on 5 and 269 DF,  p-value: < 2.2e-16

E Details. t-ratios depend on the reference level

\[ \begin{array}{l|rr|rr|rr} \hline & \text{Model 1}&& \text{Model 2}&& \text{Model 3}&\\ \hline \text{Var}& \text{Coef} & \text{t-stat} & \text{Coef} & \text{t-stat} &\text{Coef} & \text{t-stat} \\\hline logincome & 0.452 & 5.74 & 0.452 & 5.74 & 0.452 & 5.74 \\ education &0.205 & 5.30 &0.205 & 5.30&0.205 & 5.30 \\ numhh & 0.248 & 3.57 & 0.248 & 3.57 & 0.248 & 3.57 \\\hline \text{Intercept} & 3.395 & 3.77 & 2.605& 2.74 & 2.838 & 3.34\\ \text{mar=0} & -0.557 & -2.15& 0.232 & 0.44\\ \text{mar=1} & & & 0.789 & 1.59 & 0.557 & 2.15\\ \text{mar=2}& -0.789 & -1.59 & & & -0.232 & -0.44\\ \hline \end{array} \]

3.4.2 Exercise. Categorical variables and Wisconsin hospital costs

Assignment Text

This exercise examines the impact of various predictors on hospital charges. Identifying predictors of hospital charges can provide direction for hospitals, government, insurers and consumers in controlling these variables that in turn leads to better control of hospital costs. The data, from 1989, are aggregated by:

drg, diagnostic related groups of costs,
payer, type of health care provider (Fee for service, HMO, and other), and
hsa, nine major geographic areas in Wisconsin.

Some preliminary analysis of the data has already been done. In this exercise, we will analyze logcharge, the logarithm of total hospital charges per number of discharges, in terms of log_numdschg, the logarithm of the number of discharges. In the dataframe Hcost which has been loaded in advance, we restrict consideration to three types of drgs, numbers 209, 391, and 431.

Instructions

Fit a basic linear regression model using logarithmic number of discharges to predict logarithmic hospital costs and superimposed the fitted regression line on the scatter plot.
Produce a scatter plot of logarithmic number of discharges to predict logarithmic hospital costs. Allow plotting symbols and colors to vary by diagnostic related group.
Fit a MLR model using logarithmic number of discharges to predict logarithmic hospital costs, allowing intercepts and slopes to vary by diagnostic related groups.
Superimpose the fits from the MLR model on the scatter plot of logarithmic number of discharges to predict logarithmic hospital costs.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNIY29zdCA8LSByZWFkLmNzdihcIkNTVkRhdGFcXFxcV2lzY0hjb3N0cy5jc3ZcIiwgaGVhZGVyID0gVFJVRSlcbkhjb3N0IDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvMmNjMWUyNzM5YmY4MjcwOTNkYjMxZDdjNGU2ZGNkYzM0OGFjOTg0ZS9XaXNjSGNvc3RzLmNzdlwiLCBoZWFkZXIgPSBUUlVFKVxuSGNvc3QxIDwtIHN1YnNldChIY29zdCwgZHJnID09IDIwOXxkcmcgPT0gMzkxfGRyZyA9PSA0MzApIiwic2FtcGxlIjoiIyBGaXQgYSBiYXNpYyBsaW5lYXIgcmVncmVzc2lvbiBtb2RlbCB1c2luZyBsb2dhcml0aG1pYyBudW1iZXIgb2YgZGlzY2hhcmdlcyB0byBwcmVkaWN0IGxvZ2FyaXRobWljIGhvc3BpdGFsIGNvc3RzIGFuZCBzdXBlcmltcG9zZWQgdGhlIGZpdHRlZCByZWdyZXNzaW9uIGxpbmUgb24gdGhlIHNjYXR0ZXIgcGxvdC5cbmhvc3BfYmxyIDwtIGxtKGxvZ2NoYXJnZX5sb2dfbnVtZHNjaGcsIGRhdGE9SGNvc3QxKVxucGxvdChsb2djaGFyZ2V+bG9nX251bWRzY2hnLCBkYXRhPUhjb3N0MSwgeGxhYiA9IFwibG9nIG51bWJlciBkaXNjaGFyZ2VzXCIsIHlsYWIgPSBcImxvZyBjaGFyZ2VcIilcbmFibGluZShob3NwX2JsciwgY29sPVwicmVkXCIpXG5cbiMgUHJvZHVjZSBhIHNjYXR0ZXIgcGxvdCBvZiBsb2dhcml0aG1pYyBudW1iZXIgb2YgZGlzY2hhcmdlcyB0byBwcmVkaWN0IGxvZ2FyaXRobWljIGhvc3BpdGFsIGNvc3RzLiBBbGxvdyBwbG90dGluZyBzeW1ib2xzIGFuZCBjb2xvcnMgdG8gdmFyeSBieSBkaWFnbm9zdGljIHJlbGF0ZWQgZ3JvdXAuXG5wbG90KGxvZ2NoYXJnZX5sb2dfbnVtZHNjaGcsIGRhdGE9SGNvc3QxLCB4bGFiID0gXCJsb2cgbnVtYmVyIGRpc2NoYXJnZXNcIiwgeWxhYiA9IFwibG9nIGNoYXJnZVwiLFxuICAgIHBjaD0gYXMubnVtZXJpYyhhcy5mYWN0b3IoSGNvc3QxJGRyZykpLCBcbiAgICBjb2wgPSBjKFwicmVkXCIsIFwiYmxhY2tcIiwgXCJibHVlXCIpW2FzLmZhY3RvcihIY29zdDEkZHJnKV0pXG5sZWdlbmQoXCJsZWZ0XCIsIGxlZ2VuZD1jKFwiZHJnIDIwOVwiLFwiZHJnIDM5MVwiLCBcImRyZyA0MzBcIiksIGNvbD1jKFwicmVkXCIsIFwiYmxhY2tcIiwgXCJibHVlXCIpLCBwY2ggPSBjKDEsMiwzKSlcblxuIyBGaXQgYSBNTFIgbW9kZWwgYWxsb3dpbmcgaW50ZXJjZXB0cyBhbmQgc2xvcGVzIHRvIHZhcnkgYnkgZHJnLlxuaG9zcF9tbHIgPC0gbG0obG9nY2hhcmdlfmxvZ19udW1kc2NoZyArIGFzLmZhY3RvcihkcmcpKmxvZ19udW1kc2NoZywgZGF0YT1IY29zdDEpXG5cbiMgU3VwZXJpbXBvc2UgdGhlIGZpdHMgZnJvbSB0aGUgTUxSIG1vZGVsIG9uIHRoZSBzY2F0dGVyIHBsb3Qgb2YgbG9nYXJpdGhtaWMgbnVtYmVyIG9mIGRpc2NoYXJnZXMgdG8gcHJlZGljdCBsb2dhcml0aG1pYyBob3NwaXRhbCBjb3N0cy5cbnBsb3QobG9nY2hhcmdlfmxvZ19udW1kc2NoZywgZGF0YT1IY29zdDEsIHhsYWIgPSBcImxvZyBudW1iZXIgZGlzY2hhcmdlc1wiLCB5bGFiID0gXCJsb2cgY2hhcmdlXCIsXG4gICAgICAgICBwY2g9IGFzLm51bWVyaWMoYXMuZmFjdG9yKEhjb3N0MSRkcmcpKSwgXG4gICAgY29sID0gYyhcInJlZFwiLCBcImJsYWNrXCIsIFwiYmx1ZVwiKVthcy5mYWN0b3IoSGNvc3QxJGRyZyldKVxueHNlcSA8LSBzZXEoMCwxMCxsZW5ndGgub3V0PTEwMClcbmNvZWYgPC0gc3VtbWFyeShob3NwX21scikkY29lZmZpY2llbnRzWywxXVxuZml0MjA5IDwtIGNvZWZbMV0gKyBjb2VmWzJdKnhzZXFcbmxpbmVzKHhzZXEsZml0MjA5LCBjb2w9XCJyZWRcIilcbmZpdDM5MSA8LSBjb2VmWzFdICsgY29lZlszXSArIChjb2VmWzJdICsgY29lZls1XSkqeHNlcVxubGluZXMoeHNlcSxmaXQzOTEsIGNvbD1cImJsYWNrXCIpXG5maXQ0MzAgPC0gY29lZlsxXSArIGNvZWZbNF0gKyAoY29lZlsyXSArIGNvZWZbNl0pKnhzZXFcbmxpbmVzKHhzZXEsZml0NDMwLCBjb2w9XCJibHVlXCIpIiwic29sdXRpb24iOiIjcGFyKG1mcm93ID0gYygyLCAxKSlcbmhvc3BfYmxyIDwtIGxtKGxvZ2NoYXJnZX5sb2dfbnVtZHNjaGcsIGRhdGE9SGNvc3QxKVxucGxvdChsb2djaGFyZ2V+bG9nX251bWRzY2hnLCBkYXRhPUhjb3N0MSwgeGxhYiA9IFwibG9nIG51bWJlciBkaXNjaGFyZ2VzXCIsIHlsYWIgPSBcImxvZyBjaGFyZ2VcIilcbmFibGluZShob3NwX2JsciwgY29sPVwicmVkXCIpXG5cbnBsb3QobG9nY2hhcmdlfmxvZ19udW1kc2NoZywgZGF0YT1IY29zdDEsIHhsYWIgPSBcImxvZyBudW1iZXIgZGlzY2hhcmdlc1wiLCB5bGFiID0gXCJsb2cgY2hhcmdlXCIsXG4gICAgcGNoPSBhcy5udW1lcmljKGFzLmZhY3RvcihIY29zdDEkZHJnKSksIFxuICAgIGNvbCA9IGMoXCJyZWRcIiwgXCJibGFja1wiLCBcImJsdWVcIilbYXMuZmFjdG9yKEhjb3N0MSRkcmcpXSlcbmxlZ2VuZChcImxlZnRcIiwgbGVnZW5kPWMoXCJkcmcgMjA5XCIsXCJkcmcgMzkxXCIsIFwiZHJnIDQzMFwiKSwgY29sPWMoXCJyZWRcIiwgXCJibGFja1wiLCBcImJsdWVcIiksIHBjaCA9IGMoMSwyLDMpKVxuXG5ob3NwX21sciA8LSBsbShsb2djaGFyZ2V+bG9nX251bWRzY2hnICsgYXMuZmFjdG9yKGRyZykqbG9nX251bWRzY2hnLCBkYXRhPUhjb3N0MSlcbiNzdW1tYXJ5KGhvc3BfbWxyKSRjb2VmZmljaWVudHNbLDFdXG5wbG90KGxvZ2NoYXJnZX5sb2dfbnVtZHNjaGcsIGRhdGE9SGNvc3QxLCB4bGFiID0gXCJsb2cgbnVtYmVyIGRpc2NoYXJnZXNcIiwgeWxhYiA9IFwibG9nIGNoYXJnZVwiLFxuICAgICAgICAgcGNoPSBhcy5udW1lcmljKGFzLmZhY3RvcihIY29zdDEkZHJnKSksIFxuICAgIGNvbCA9IGMoXCJyZWRcIiwgXCJibGFja1wiLCBcImJsdWVcIilbYXMuZmFjdG9yKEhjb3N0MSRkcmcpXSlcbnhzZXEgPC0gc2VxKDAsMTAsbGVuZ3RoLm91dD0xMDApXG5jb2VmIDwtIHN1bW1hcnkoaG9zcF9tbHIpJGNvZWZmaWNpZW50c1ssMV1cbmZpdDIwOSA8LSBjb2VmWzFdICsgY29lZlsyXSp4c2VxXG5saW5lcyh4c2VxLGZpdDIwOSwgY29sPVwicmVkXCIpXG5maXQzOTEgPC0gY29lZlsxXSArIGNvZWZbM10gKyAoY29lZlsyXSArIGNvZWZbNV0pKnhzZXFcbmxpbmVzKHhzZXEsZml0MzkxLCBjb2w9XCJibGFja1wiKVxuZml0NDMwIDwtIGNvZWZbMV0gKyBjb2VmWzRdICsgKGNvZWZbMl0gKyBjb2VmWzZdKSp4c2VxXG5saW5lcyh4c2VxLGZpdDQzMCwgY29sPVwiYmx1ZVwiKSIsInNjdCI6InN1Y2Nlc3NfbXNnKFwiQ29uZ3JhdHVsYXRpb25zISBXaGVuIHlvdSBzdXBlcmltcG9zZWQgdGhlIGZpdHMgZnJvbSB0aGUgTUxSIG1vZGVsIG9uIHRoZSBzY2F0dGVyIHBsb3Qgb2YgbG9nYXJpdGhtaWMgbnVtYmVyIG9mIGRpc2NoYXJnZXMgdG8gcHJlZGljdCBsb2dhcml0aG1pYyBob3NwaXRhbCBjb3N0cywgbm90ZSBob3cgc2xvcGVzIGRpZmZlciBkcmFtYXRpY2FsbHkgZnJvbSB0aGUgc2xvcGUgZnJvbSB0aGUgYmFzaWMgbGluZWFyIHJlZ3Jlc3Npb24gbW9kZWwuXCIpIiwiaGludCI6IlRoZXJlIGlzIGN1cnJlbnRseSBub3RoaW5nIHRvIGNoYW5nZSBpbiB0aGlzIHR1dG9yaWFsISBTaW1wbHkgbG9vayBvdmVyIHRoZSBjb2RlIGFuZCB0cnkgdG8gdW5kZXJzdGFuZCB3aGF0IGVhY2ggbGluZSBkb2VzLiJ9

3.5 General linear hypothesis

In this section, you learn how to:

Jointly test the significance of a set of regression coefficients using the general linear hypothesis
Conduct a test of a regression coefficient versus one- or two-side alternatives

3.5.1 Video

Video Overhead Details

A Details. Testing the significance of a categorical variable

#Term <- read.csv("CSVData\\term_life.csv", header = TRUE)
Term <- read.csv("https://assets.datacamp.com/production/repositories/2610/datasets/efc64bc2d78cf6b48ad2c3f5e31800cb773de261/term_life.csv", header = TRUE)
Term1 <- subset(Term, subset = face > 0)
Term4 <- Term1[,c("numhh", "education", "logincome", "marstat", "logface")]
Term_mlr1 <- lm(logface ~ logincome + education + numhh + as.factor(Term4$marstat), data = Term4)
anova(Term_mlr1)
Term_mlr2 <- lm(logface ~ logincome + education + numhh, data = Term4)

Fstat <- (anova(Term_mlr2)$`Sum Sq`[4] - anova(Term_mlr1)$`Sum Sq`[5])/(2*anova(Term_mlr1)$`Mean Sq`[5])
Fstat
cat("p-value is", 1 - pf(Fstat, df1 = 2 , df2 = anova(Term_mlr1)$Df[5]))

Analysis of Variance Table

Response: logface
                          Df Sum Sq Mean Sq F value    Pr(>F)    
logincome                  1 222.63 222.629  97.280 < 2.2e-16 ***
education                  1  51.50  51.502  22.504 3.407e-06 ***
numhh                      1  54.34  54.336  23.743 1.883e-06 ***
as.factor(Term4$marstat)   2  14.81   7.406   3.236   0.04085 *  
Residuals                269 615.62   2.289                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
[1] 3.236048
p-value is 0.04085475

B Details. Overview of the general linear hypothesis

The likelihood ratio is a general statistical test procedure that compares a model to a subset
The general linear hypothesis test procedure is similar.
- Start with a (large) linear regression model, examine the fit to a set of data
- Compare this to smaller model that is a subset of the large model.
- “Subset” is the sense that regression coefficients from the small model are linear combinations of regression coefficients of the large model (e.g., set them to zero)
Although the likelihood ratio test is more generally available, the general linear hypothesis test is more accurate for smaller data sets (for normally distributed data)

C Details. Procedure for conducting the general linear hypothesis

Run the full regression and get the error sum of squares and mean square error, which we label as $(Error SS)_{full}$ and $s^2_{full}$, respectively.
Run a reduced regression and get the error sum of squares, labelled $(Error SS)_{reduced}$.
Using $p$ for the number of linear restrictions, calculate \[ F-ratio = \frac{(Error SS)_{reduced}-(Error SS)_{full}}{p s^2_{full}} . \]
The probability value is $p-value = \Pr(F_{p,df} > F-ratio)$ where $F_{p,df}$ has an F distribution with degrees of freedom p and df, respectively. (Here, df is the degrees of freedom for the full model.)

D Details. The general linear hypothesis for a single variable

Suppose that you wish to test the hypothesisthat a regression coefficient equals 0.
- One could use the general linear hypothsis procedure with $p=1$.
- One could also examine the corresponding $t-ratio$.
- Which is correct?
Both. One can show that $(t-ratio)^2 = F-ratio$, so they are equivalent statistics.
- The general linear hypothesis is useful because it can be extended to multiple coefficients.
- The t-ratio is useful because it can be used to examine one-sided alternative hypotheses.

3.5.2 Exercise. Hypothesis testing and term life

Assignment Text

With our Term life data, let us compare a model based on the binary variable that indicates whether a survey respondent is single versus the more complex marital status, marstat. In principle, more detailed information is better. But, it may be that the additional information in marstat, compared to single, does not help fit the data in a significantly better way.

As part of the preparatory work, the dataframe Term4 is available that includes the binary variable single and the factor marstat. Moreover, the regression object Term_mlr contains information in a multiple linear regression fit of logface on the base explanatory variables ’logincome,education, andnumhh`.

Instructions

Fit a MLR model using the base explanatory variables plus single and another model using the base variables plus marstat.
Use the F test to decide whether the additional complexity marstat is warranted by calculating the p-value associated with this test.
Fit a MLR model using the base explanatory variables plus single interacted with logincome and another model using the base variables plus marstat interacted with logincome.
Use the F test to decide whether the additional complexity marstat is warranted by calculating the p-value associated with this test.

Hint

Here is the code to calculate it by hand
Fstat12 <- (anova(Term_mlr1)$`Sum Sq`[5] - 
              anova(Term_mlr2)$`Sum Sq`[5])/(1*anova(Term_mlr2)$`Mean Sq`[5])
Fstat12
cat("p-value is", 1 - pf(Fstat12, df1 = 1 , df2 = anova(Term_mlr2)$Df[5]))

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNUZXJtIDwtIHJlYWQuY3N2KFwiQ1NWRGF0YVxcXFx0ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvZWZjNjRiYzJkNzhjZjZiNDhhZDJjM2Y1ZTMxODAwY2I3NzNkZTI2MS90ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtMSA8LSBzdWJzZXQoVGVybSwgc3Vic2V0ID0gZmFjZSA+IDApXG5UZXJtNCA8LSBUZXJtMVssYyhcIm51bWhoXCIsIFwiZWR1Y2F0aW9uXCIsIFwibG9naW5jb21lXCIsIFwibWFyc3RhdFwiLCBcImxvZ2ZhY2VcIildXG5UZXJtNCRzaW5nbGUgPC0gMSooVGVybTQkbWFyc3RhdCA9PSAwKVxuVGVybTQkbWFyc3RhdCA8LSBhcy5mYWN0b3IoVGVybTQkbWFyc3RhdClcblRlcm1fbWxyIDwtIGxtKGxvZ2ZhY2UgfiBsb2dpbmNvbWUgKyBlZHVjYXRpb24gKyBudW1oaCAsIGRhdGEgPSBUZXJtNClcbmFub3ZhKFRlcm1fbWxyKSIsInNhbXBsZSI6IiMgRml0IGEgTUxSIG1vZGVsIHVzaW5nIHRoZSBiYXNlIGV4cGxhbmF0b3J5IHZhcmlhYmxlcyBwbHVzIGBzaW5nbGVgIGFuZCBhbm90aGVyIG1vZGVsIHVzaW5nIHRoZSBiYXNlIHZhcmlhYmxlcyBwbHVzIGBtYXJzdGF0YC5cblRlcm1fbWxyMSA8LSBsbShsb2dmYWNlIH4gbG9naW5jb21lICsgZWR1Y2F0aW9uICsgbnVtaGggK3NpbmdsZSwgZGF0YSA9IFRlcm00KVxuVGVybV9tbHIyIDwtIGxtKGxvZ2ZhY2UgfiBsb2dpbmNvbWUgKyBlZHVjYXRpb24gKyBudW1oaCArbWFyc3RhdCwgZGF0YSA9IFRlcm00KVxuXG4jIFVzZSB0aGUgRiB0ZXN0IHRvIGRlY2lkZSB3aGV0aGVyIHRoZSBhZGRpdGlvbmFsIGNvbXBsZXhpdHkgYG1hcnN0YXRgIGlzIHdhcnJhbnRlZCBieSBjYWxjdWxhdGluZyB0aGUgcC12YWx1ZSBhc3NvY2lhdGVkIHdpdGggdGhpcyB0ZXN0LlxuYW5vdmEoVGVybV9tbHIxLFRlcm1fbWxyMilcblxuIyBGaXQgYSBNTFIgbW9kZWwgdXNpbmcgdGhlIGJhc2UgZXhwbGFuYXRvcnkgdmFyaWFibGVzIHBsdXMgYHNpbmdsZWAgaW50ZXJhY3RlZCB3aXRoIGBsb2dpbmNvbWVgIGFuZCBhbm90aGVyIG1vZGVsIHVzaW5nIHRoZSBiYXNlIHZhcmlhYmxlcyBwbHVzIGBtYXJzdGF0YCBpbnRlcmFjdGVkIHdpdGggYGxvZ2luY29tZWAuXG5UZXJtX21scjMgPC0gbG0obG9nZmFjZSB+IGxvZ2luY29tZSArIGVkdWNhdGlvbiArIG51bWhoICsgc2luZ2xlKmxvZ2luY29tZSwgZGF0YSA9IFRlcm00KVxuVGVybV9tbHI0IDwtIGxtKGxvZ2ZhY2UgfiBsb2dpbmNvbWUgKyBlZHVjYXRpb24gKyBudW1oaCArbWFyc3RhdCpsb2dpbmNvbWUsIGRhdGEgPSBUZXJtNClcblxuIyBVc2UgdGhlIEYgdGVzdCB0byBkZWNpZGUgd2hldGhlciB0aGUgYWRkaXRpb25hbCBjb21wbGV4aXR5IGBtYXJzdGF0YCBpcyB3YXJyYW50ZWQgYnkgY2FsY3VsYXRpbmcgdGhlIHAtdmFsdWUgYXNzb2NpYXRlZCB3aXRoIHRoaXMgdGVzdC5cbmFub3ZhKFRlcm1fbWxyMyxUZXJtX21scjQpIiwic29sdXRpb24iOiJUZXJtX21scjEgPC0gbG0obG9nZmFjZSB+IGxvZ2luY29tZSArIGVkdWNhdGlvbiArIG51bWhoICtzaW5nbGUsIGRhdGEgPSBUZXJtNClcblRlcm1fbWxyMiA8LSBsbShsb2dmYWNlIH4gbG9naW5jb21lICsgZWR1Y2F0aW9uICsgbnVtaGggK21hcnN0YXQsIGRhdGEgPSBUZXJtNClcbmFub3ZhKFRlcm1fbWxyMSxUZXJtX21scjIpXG4jRnN0YXQxMiA8LSAoYW5vdmEoVGVybV9tbHIxKSRgU3VtIFNxYFs1XSAtIFxuIyAgICAgICAgICAgICAgYW5vdmEoVGVybV9tbHIyKSRgU3VtIFNxYFs1XSkvKDEqYW5vdmEoVGVybV9tbHIyKSRgTWVhbiBTcWBbNV0pXG4jRnN0YXQxMlxuI2NhdChcInAtdmFsdWUgaXNcIiwgMSAtIHBmKEZzdGF0MTIsIGRmMSA9IDEgLCBkZjIgPSBhbm92YShUZXJtX21scjIpJERmWzVdKSlcblRlcm1fbWxyMyA8LSBsbShsb2dmYWNlIH4gbG9naW5jb21lICsgZWR1Y2F0aW9uICsgbnVtaGggKyBzaW5nbGUqbG9naW5jb21lLCBkYXRhID0gVGVybTQpXG5UZXJtX21scjQgPC0gbG0obG9nZmFjZSB+IGxvZ2luY29tZSArIGVkdWNhdGlvbiArIG51bWhoICttYXJzdGF0KmxvZ2luY29tZSwgZGF0YSA9IFRlcm00KVxuYW5vdmEoVGVybV9tbHIzLFRlcm1fbWxyNCkiLCJzY3QiOiJleCgpICU+JSBjaGVja19vYmplY3QoXCJUZXJtX21scjFcIiAsIHVuZGVmaW5lZF9tc2c9XCJVc2UgYGxtYCB0byBjcmVhdGUgYSBsaW5lYXIgbW9kZWwgYW5kIHN0b3JlIGl0IHVuZGVyIHRoZSBuYW1lIGBUZXJtX21scjFgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIllvdXIgbW9kZWwgc2hvdWxkIGV4cGxhaW4gYGxvZ2ZhY2VgIGJhc2VkIG9uIGBsb2dpbmNvbWVgLCBgZWR1Y2F0aW9uYCwgYG51bWhoYCwgYW5kIGBzaW5nbGVgIGZyb20gdGhlIGRhdGEgc2V0IGBUZXJtNGAuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJUZXJtX21scjJcIiAsIHVuZGVmaW5lZF9tc2c9XCJVc2UgYGxtYCB0byBjcmVhdGUgYSBsaW5lYXIgbW9kZWwgYW5kIHN0b3JlIGl0IHVuZGVyIHRoZSBuYW1lIGBUZXJtX21scjJgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIllvdXIgbW9kZWwgc2hvdWxkIGV4cGxhaW4gYGxvZ2ZhY2VgIGJhc2VkIG9uIGBsb2dpbmNvbWVgLCBgZWR1Y2F0aW9uYCwgYG51bWhoYCwgYW5kIGBtYXJzdGF0YCBmcm9tIHRoZSBkYXRhIHNldCBgVGVybTRgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJhbm92YVwiLGluZGV4PTEsIG5vdF9jYWxsZWRfbXNnPVwiUnVuIGFuIGFub3ZhIHRlc3QgdG8gY29tcGFyZSB0aGUgdHdvIG1vZGVscyB3ZSBqdXN0IGNyZWF0ZWQuIFwiKSAlPiUgY2hlY2tfcmVzdWx0KCkgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJZb3Ugc2hvdWxkIHJ1biB0aGUgYGFub3ZhYCB0ZXN0IG9uIGBUZXJtX21scjFgIGFuZCBgVGVybV9tbHIyYC5cIilcbmV4KCkgJT4lIGNoZWNrX29iamVjdChcIlRlcm1fbWxyM1wiICwgdW5kZWZpbmVkX21zZz1cIlVzZSBgbG1gIHRvIGNyZWF0ZSBhIGxpbmVhciBtb2RlbCBhbmQgc3RvcmUgaXQgdW5kZXIgdGhlIG5hbWUgYFRlcm1fbWxyM2AuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiWW91ciBtb2RlbCBzaG91bGQgZXhwbGFpbiBgbG9nZmFjZWAgYmFzZWQgb24gYGxvZ2luY29tZWAsIGBlZHVjYXRpb25gLCBgbnVtaGhgLCBhbmQgdGhlIHByb2R1Y3Qgb2YgYHNpbmdsZWAgYW5kIGBsb2dpbmNvbWVgIGZyb20gdGhlIGRhdGEgc2V0IGBUZXJtNGAuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJUZXJtX21scjRcIiAsIHVuZGVmaW5lZF9tc2c9XCJVc2UgYGxtYCB0byBjcmVhdGUgYSBsaW5lYXIgbW9kZWwgYW5kIHN0b3JlIGl0IHVuZGVyIHRoZSBuYW1lIGBUZXJtX21scjRgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIllvdXIgbW9kZWwgc2hvdWxkIGV4cGxhaW4gYGxvZ2ZhY2VgIGJhc2VkIG9uIGBsb2dpbmNvbWVgLCBgZWR1Y2F0aW9uYCwgYG51bWhoYCwgYW5kIHRoZSBwcm9kdWN0IG9mIGBtYXJzdGF0YCBhbmQgYGxvZ2luY29tZWAgZnJvbSB0aGUgZGF0YSBzZXQgYFRlcm00YC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwiYW5vdmFcIixpbmRleD0yLCBub3RfY2FsbGVkX21zZz1cIlJ1biBhbiBhbm92YSB0ZXN0IHRvIGNvbXBhcmUgdGhlIHR3byBuZXcgbW9kZWxzIHdlIGp1c3QgY3JlYXRlZC4gXCIpICU+JSBjaGVja19yZXN1bHQoKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIllvdSBzaG91bGQgcnVuIHRoZSBgYW5vdmFgIHRlc3Qgb24gYFRlcm1fbWxyM2AgYW5kIGBUZXJtX21scjRgLlwiKVxuc3VjY2Vzc19tc2coXCJDb25ncmF0dWxhdGlvbnMhIEh5cG90aGVzaXMgdGVzdGluZyBpcyBhIHByaW1hcnkgdG9vbCBmb3IgICdpbmZlcnJpbmcnIGFib3V0IHRoZSByZWFsIHdvcmxkIHtpbiBjb250cmFzdCB0byBtYXRoZW1hdGljYWwgJ2RlZHVjdGlvbicufSBNb3Jlb3ZlciwgYXMgd2Ugd2lsbCBzZWUgaW4gdGhlIG5leHQgY2hhcHRlciwgaXQgY2FuIGFsc28gYmUgdXNlZCB0byBkZXZlbG9wIGEgbW9kZWwuXCIpICAiLCJoaW50IjoiSGVyZSBpcyB0aGUgY29kZSB0byBjYWxjdWxhdGUgaXQgYnkgaGFuZCJ9

3.5.3 Exercise. Hypothesis testing and Wisconsin hospital costs

Assignment Text

In a previous exercise, you were introduced to a dataset with hospital charges aggregated by:

drg, diagnostic related groups of costs,
payer, type of health care provider (Fee for service, HMO, and other), and
hsa, nine major geographic areas.

We continue our analysis of the outcome variable logcharge, the logarithm of total hospital charges per number of discharges, in terms of log_numdschg, the logarithm of the number of discharges, as well as the three categorical variables used in the aggregation. As before, we restrict consideration to three types of drgs, numbers 209, 391, and 431 that has been preloaded in the dataframe Hcost1.

Instructions

Fit a basic linear regression model using logarithmic hospital costs as the outcome variable and explanatory variable logarithmic number of discharges.
Fit a MLR model using logarithmic hospital costs as the outcome variable and explanatory variables logarithmic number of discharges and the categorical variable diagnostic related group. Identify the F statistic and p value that test the importance of diagnostic related group.
Fit a MLR model using logarithmic hospital costs as the outcome variable and explanatory variable logarithmic number of discharges interacted with diagnostic related group. Identify the F statistic and p value that test the importance of diagnostic related group interaction with logarithmic number of discharges.
Calculate a coefficient of determination, $R^2$, for each of these models as well as for a model using logarithmic number of discharges and categorical variable hsa as predictors.

3.5.4 Exercise. Hypothesis testing and auto claims

Assignment Text

As an actuarial analyst, you are working with a large insurance company to help them understand their claims distribution for their private passenger automobile policies. You have available claims data for a recent year, consisting of:

state: codes 01 through 17 used, with each code randomly assigned to an actual individual state
class: rating class of operator, based on age, gender, marital status, and use of vehicle
gender: operator gender
age: operator age
paid: amount paid to settle and close a claim.

You are focusing on older drivers, 50 and higher, for which there are n = 6,773 claims available.

Instructions

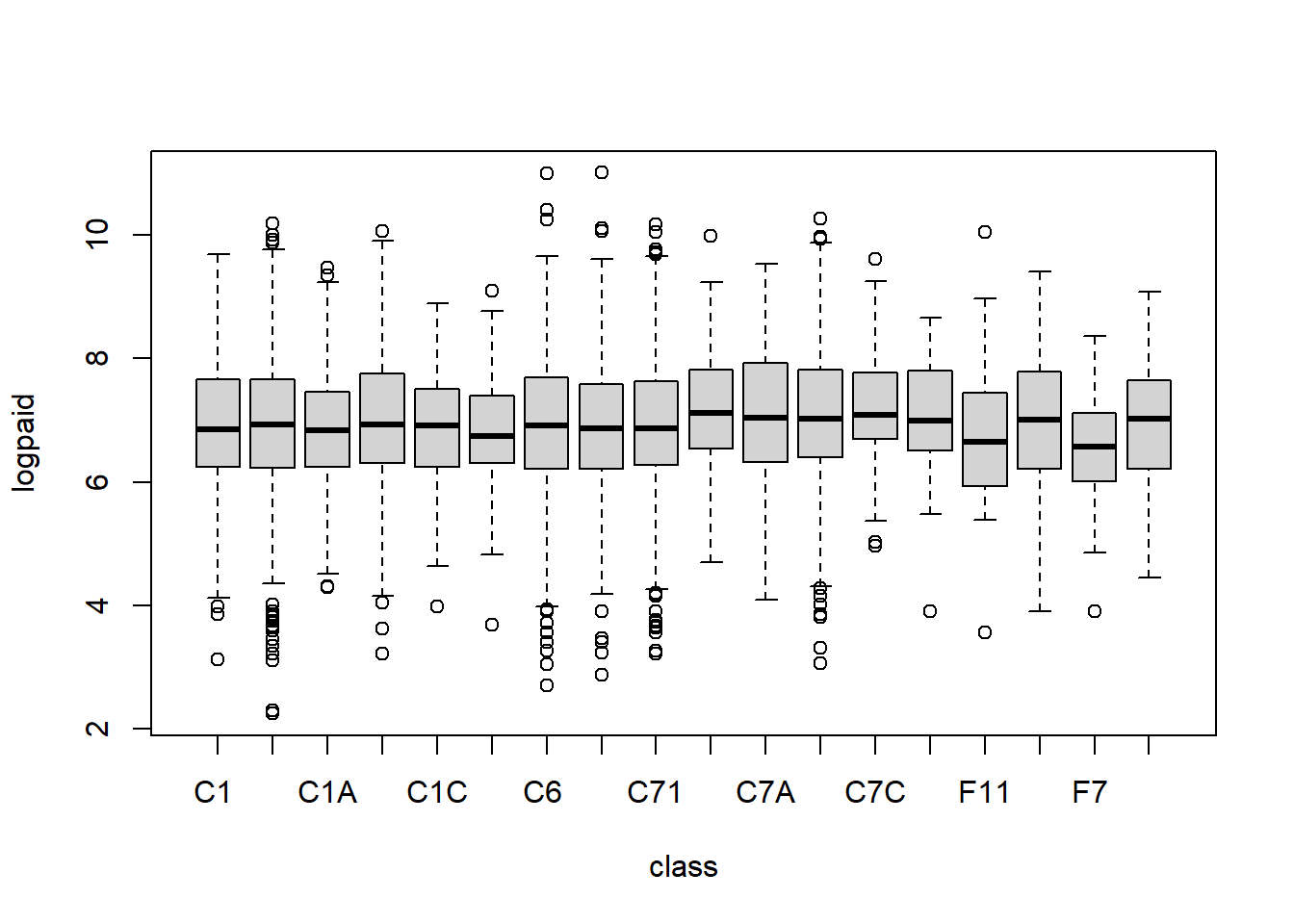
Run a regression of logpaid on age. Is age a statistically significant variable? To respond to this question, use a formal test of hypothesis. State your null and alternative hypotheses, decision-making criterion, and your decision-making rule. Also comment on the goodness of fit of this variable.
Consider using class as a single explanatory variable. Use the one factor to estimate the model and respond to the following questions.

b (i). What is the point estimate of claims in class C7, drivers 50-69, driving to work or school, less than 30 miles per week with annual mileage under 7500, in natural logarithmic units?

b (ii). Determine the corresponding 95% confidence interval of expected claims, in natural logarithmic units.

b (iii). Convert the 95% confidence interval of expected claims that you determined in part b(ii) to dollars.
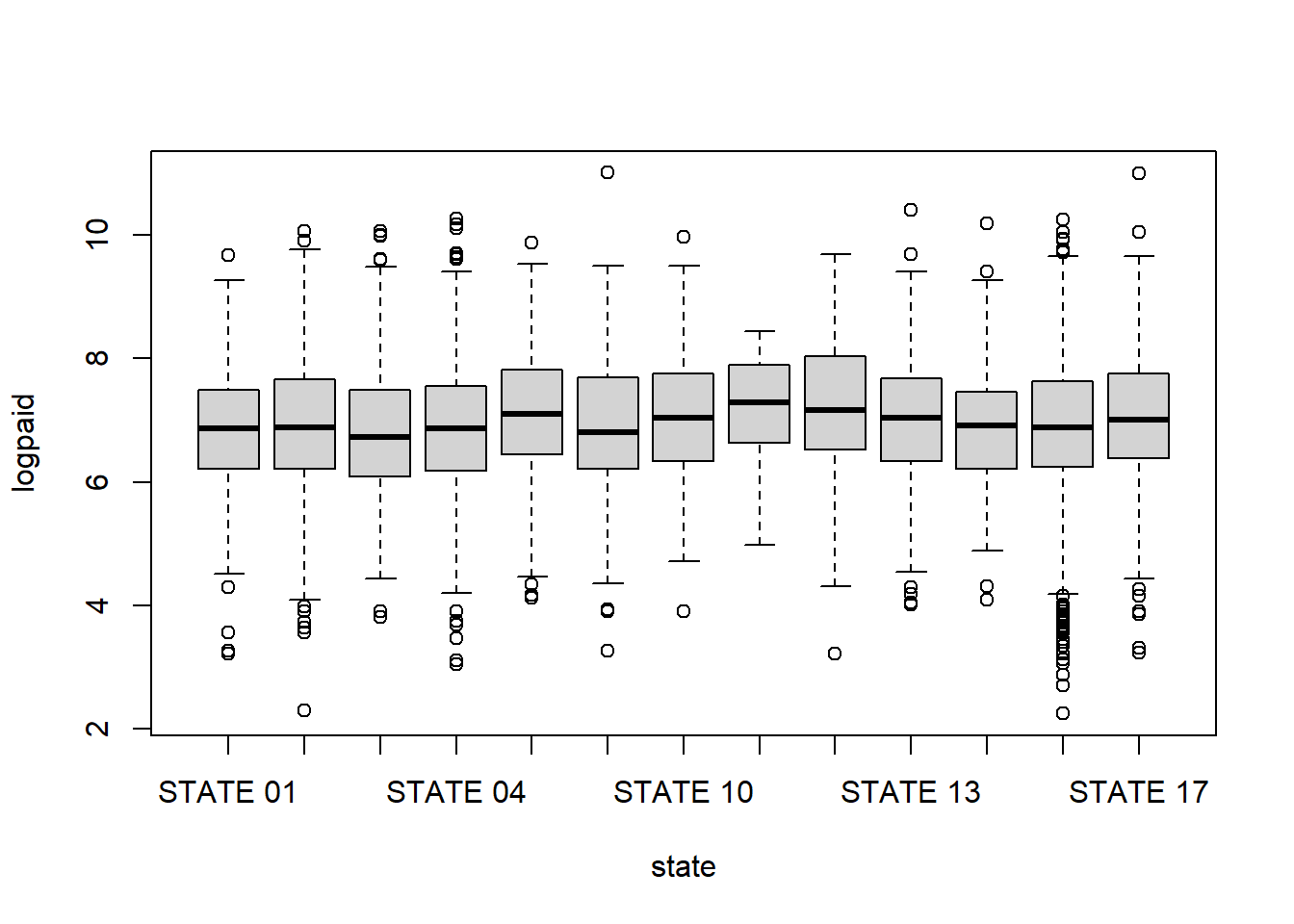
Run a regression of logpaid on age, gender and the categorical variables state and class.

c (i). Is gender a statistically significant variable? To respond to this question, use a formal test of hypothesis. State your null and alternative hypotheses, decision-making criterion, and your decision-making rule.

c (ii). Is class a statistically significant variable? To respond to this question, use a formal test of hypothesis. State your null and alternative hypotheses, decision-making criterion, and your decision-making rule.

c (iii). Use the model to provide a point estimate of claims in dollars (not log dollars) for a male age 60 in STATE 2 in class C7.

c (iv). Write down the coefficient associated with class C7 and interpret this coefficient.


Call:
lm(formula = logpaid ~ class, data = AutoC)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7002 -0.6912 -0.0437  0.7128  4.1009 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.940938   0.039699 174.838   <2e-16 ***
classC11     0.010564   0.050696   0.208   0.8349    
classC1A    -0.075432   0.128202  -0.588   0.5563    
classC1B     0.057420   0.065380   0.878   0.3798    
classC1C    -0.154707   0.178007  -0.869   0.3848    
classC2     -0.139442   0.142595  -0.978   0.3282    
classC6     -0.015057   0.053217  -0.283   0.7772    
classC7     -0.039775   0.053191  -0.748   0.4546    
classC71     0.012730   0.050887   0.250   0.8025    
classC72     0.241716   0.122626   1.971   0.0487 *  
classC7A     0.122755   0.108174   1.135   0.2565    
classC7B     0.131512   0.056956   2.309   0.0210 *  
classC7C     0.302596   0.125307   2.415   0.0158 *  
classF1      0.062962   0.202561   0.311   0.7559    
classF11    -0.136891   0.173726  -0.788   0.4307    
classF6     -0.030546   0.094148  -0.324   0.7456    
classF7     -0.363874   0.144807  -2.513   0.0120 *  
classF71    -0.005476   0.117810  -0.046   0.9629    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.07 on 6755 degrees of freedom
Multiple R-squared:  0.005048,  Adjusted R-squared:  0.002544 
F-statistic: 2.016 on 17 and 6755 DF,  p-value: 0.00786


Call:
lm(formula = logpaid ~ state, data = AutoC)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.6555 -0.6847 -0.0415  0.7005  4.0788 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)    6.82202    0.08286  82.328  < 2e-16 ***
stateSTATE 02  0.11739    0.08878   1.322 0.186133    
stateSTATE 03  0.02224    0.10071   0.221 0.825246    
stateSTATE 04  0.05195    0.09262   0.561 0.574893    
stateSTATE 06  0.30735    0.09327   3.295 0.000988 ***
stateSTATE 07  0.10127    0.10537   0.961 0.336562    
stateSTATE 10  0.21247    0.10486   2.026 0.042787 *  
stateSTATE 11  0.17462    0.36540   0.478 0.632751    
stateSTATE 12  0.40876    0.10715   3.815 0.000138 ***
stateSTATE 13  0.21792    0.11111   1.961 0.049890 *  
stateSTATE 14  0.06485    0.11667   0.556 0.578297    
stateSTATE 15  0.08479    0.08596   0.986 0.323956    
stateSTATE 17  0.22406    0.09585   2.338 0.019442 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.068 on 6760 degrees of freedom
Multiple R-squared:  0.008109,  Adjusted R-squared:  0.006348 
F-statistic: 4.606 on 12 and 6760 DF,  p-value: 1.749e-07

Analysis of Variance Table

Response: logpaid
            Df Sum Sq Mean Sq F value    Pr(>F)    
state       12   63.0  5.2495  4.6055 1.749e-07 ***
Residuals 6760 7705.2  1.1398                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Call:
lm(formula = logpaid ~ class + state + age + gender, data = AutoC)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7266 -0.6802 -0.0433  0.7072  4.1809 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)    6.974923   0.140144  49.770  < 2e-16 ***
classC11       0.055573   0.051695   1.075 0.282410    
classC1A      -0.110591   0.128238  -0.862 0.388506    
classC1B       0.022671   0.066388   0.341 0.732740    
classC1C      -0.160355   0.178056  -0.901 0.367842    
classC2       -0.183935   0.142784  -1.288 0.197719    
classC6        0.057560   0.058767   0.979 0.327395    
classC7       -0.021854   0.054531  -0.401 0.688605    
classC71       0.024622   0.053049   0.464 0.642569    
classC72       0.260057   0.123451   2.107 0.035192 *  
classC7A       0.119315   0.108879   1.096 0.273183    
classC7B       0.124196   0.059098   2.102 0.035634 *  
classC7C       0.299023   0.126300   2.368 0.017934 *  
classF1        0.130054   0.202380   0.643 0.520491    
classF11      -0.058684   0.174394  -0.337 0.736503    
classF6        0.068612   0.098270   0.698 0.485079    
classF7       -0.309974   0.145271  -2.134 0.032898 *  
classF71       0.029459   0.118848   0.248 0.804239    
stateSTATE 02  0.098538   0.089280   1.104 0.269765    
stateSTATE 03  0.006302   0.101050   0.062 0.950272    
stateSTATE 04  0.019266   0.093712   0.206 0.837118    
stateSTATE 06  0.283853   0.094105   3.016 0.002568 ** 
stateSTATE 07  0.076593   0.106361   0.720 0.471475    
stateSTATE 10  0.181802   0.105448   1.724 0.084739 .  
stateSTATE 11  0.172272   0.365574   0.471 0.637487    
stateSTATE 12  0.388006   0.108333   3.582 0.000344 ***
stateSTATE 13  0.188491   0.111980   1.683 0.092371 .  
stateSTATE 14  0.068141   0.116720   0.584 0.559373    
stateSTATE 15  0.065570   0.086624   0.757 0.449110    
stateSTATE 17  0.199398   0.096914   2.057 0.039680 *  
age           -0.003021   0.001690  -1.787 0.073914 .  
genderM        0.038953   0.026907   1.448 0.147747    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.066 on 6741 degrees of freedom
Multiple R-squared:  0.01365,   Adjusted R-squared:  0.009113 
F-statistic: 3.009 on 31 and 6741 DF,  p-value: 4.354e-08

Analysis of Variance Table

Response: logpaid
            Df Sum Sq Mean Sq F value    Pr(>F)    
class       17   39.2  2.3066  2.0293  0.007346 ** 
state       12   61.0  5.0841  4.4728 3.354e-07 ***
age          1    3.4  3.4284  3.0162  0.082480 .  
gender       1    2.4  2.3823  2.0958  0.147747    
Residuals 6741 7662.2  1.1367                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1