Chapter 4 Variable Selection

Chapter description

This chapter describes tools and techniques to help you select variables to enter into a linear regression model, beginning with an iterative model selection process. In applications with many potential explanatory variables, automatic variable selection procedures are available that will help you quickly evaluate many models. Nonetheless, automatic procedures have serious limitations including the inability to account properly for nonlinearities such as the impact of unusual points; this chapter expands upon the Chapter 2 discussion of unusual points. It also describes collinearity, a common feature of regression data where explanatory variables are linearly related to one another. Other topics that impact variable selection, including out-of-sample validation, are also introduced.

4.1 An iterative approach to data analysis and modeling

In this section, you learn how to:

Describe the iterative approach to data analysis and modeling.

4.1.1 Video

Video Overhead Details

A Details. Iterative approach

Model formulation stage
Fitting
Diagnostic checking - the data and model must be consistent with one another before additional inferences can be made.

plot.new()
par(mar=c(0,0,0,0), cex=0.9)
plot.window(xlim=c(0,18),ylim=c(-5,5))

text(1,3,labels="DATA",adj=0, cex=0.8)
text(1,0,labels="PLOTS",adj=0, cex=0.8)
text(1,-3,labels="THEORY",adj=0, cex=0.8)
text(3.9,0,labels="MODEL\nFORMULATION",adj=0, cex=0.8)
text(8.1,0,labels="FITTING",adj=0, cex=0.8)
text(11,0,labels="DIAGNOSTIC\nCHECKING",adj=0, cex=0.8)
text(15,0,labels="INFERENCE",adj=0, cex=0.8)
text(14.1,0.5,labels="OK",adj=0, cex=0.6)

rect(0.8,2.0,2.6,4.0)
arrows(1.7,2.0,1.7,1.0,code=2,lwd=2,angle=25,length=0.10)
rect(0.8,-1.0,2.6,1.0)
arrows(1.7,-2.0,1.7,-1.0,code=2,lwd=2,angle=25,length=0.10)
rect(0.8,-4.0,2.6,-2.0)

arrows(2.6,0,3.2,0,code=2,lwd=2,angle=25,length=0.10)

x<-c(5,7.0,5,3.2)
y<-c(2,0,-2,0)
polygon(x,y)
arrows(7.0,0,8.0,0,code=2,lwd=2,angle=25,length=0.10)

rect(8.0,-1.0,9.7,1.0)
arrows(9.7,0,10.2,0,code=2,lwd=2,angle=25,length=0.10)

x1<-c(12,14.0,12,10.2)
y1<-c(2,0,-2,0)
polygon(x1,y1)
arrows(14.0,0,14.8,0,code=2,lwd=2,angle=25,length=0.10)

rect(14.8,-1.0,17.5,1.0)
arrows(12,-2.0,12,-3,code=2,lwd=2,angle=25,length=0.10)
arrows(12,-3.0,5,-3,code=2,lwd=2,angle=25,length=0.10)
arrows(5,-3.0,5,-2,code=2,lwd=2,angle=25,length=0.10)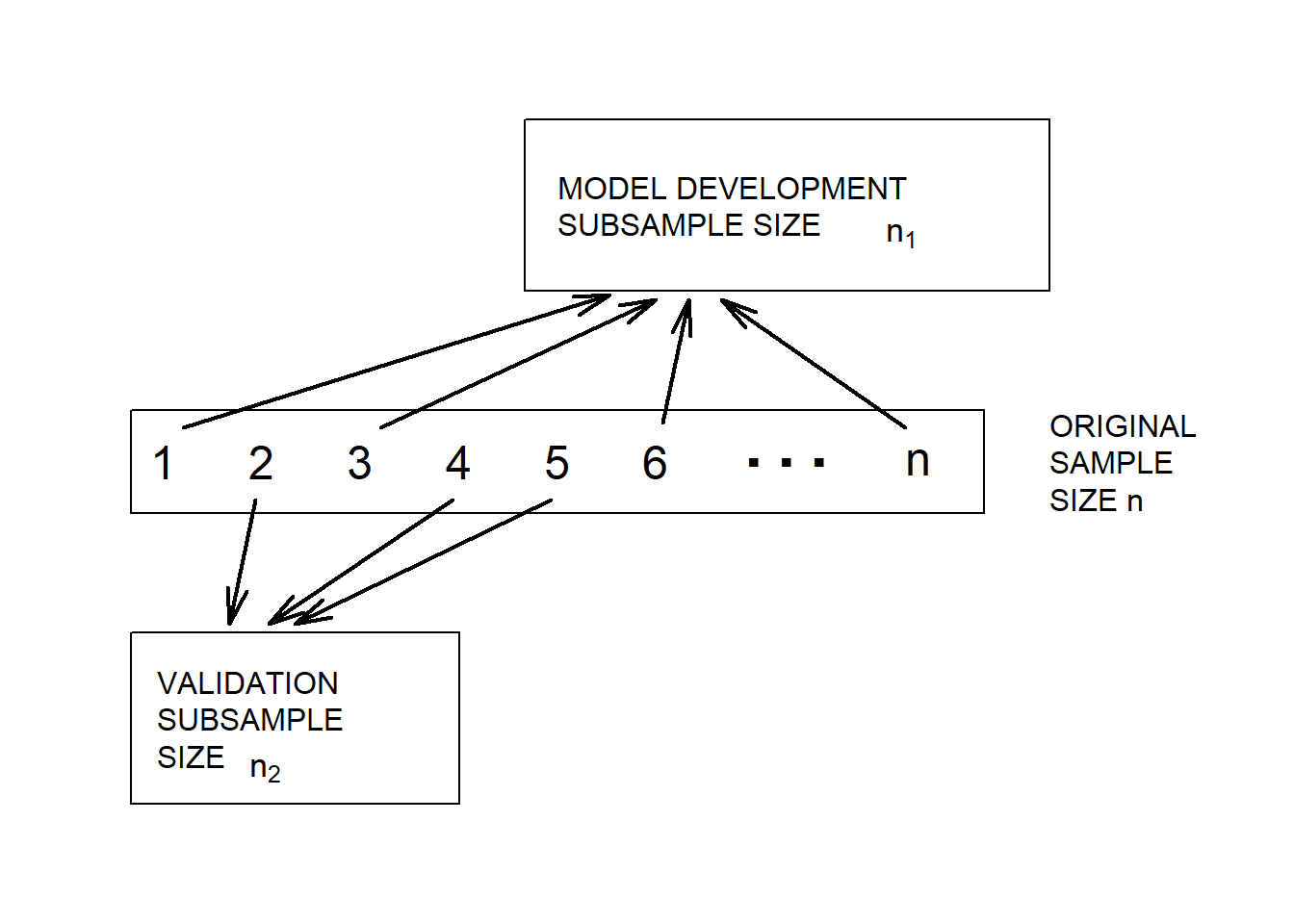

B Details. Many possible models

\[ \begin{array}{l|r} \hline \text{E }y = \beta _{0} & \text{1 model with no variables } \\ \text{E }y = \beta _{0}+\beta_1 x_{i}, & \text{4 models with one variable} \\ \text{E }y = \beta _{0}+\beta_1 x_{i}+\beta_{2} x_{j}, & \text{6 models with two variables} \\ \text{E }y = \beta _{0}+\beta_{1} x_{1}+\beta_{2} x_{j} +\beta_{3} x_{k},& \text{4 models with three variables} \\ \text{E }y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} +\beta_{3} x_{3}+\beta_{4} x_{4} & \text{1 model with all variables} \\ \hline \end{array} \]

With k explanatory variables, there are $2^k$ possible linear models
There are infinitely many nonlinear ones!!

C Details. Model validation

Model validation is the process of confirming our proposed model.
Concern: data-snooping - fitting many models to a single set of data.
- Response to concern: out-of-sample validation.
- Divide the data into model development, or training and validation, or test, subsamples.

par(mai=c(0,0.1,0,0))
plot.new()
plot.window(xlim=c(0,18),ylim=c(-10,10))
rect(1,-1.2,14,1.2)
rect(7,4,15,8)
rect(1,-8,6,-4)
x<-seq(1.5,9,length=6)
y<-rep(0,6)
text(x,y,labels=c(1:6),cex=1.5)
x1<-seq(10.5,11.5,length=3)
y1<-rep(0,3)
text(x1,y1,labels=rep(".",3),cex=3)
text(13,0,labels="n",cex=1.5)

text(15,0,labels="ORIGINAL\nSAMPLE\nSIZE n",adj=0)
text(7.5,6,labels="MODEL DEVELOPMENT\nSUBSAMPLE SIZE",adj=0)
text(12.5,5.3, expression(n[1]), adj=0, cex=1.1)
text(1.4,-6,labels="VALIDATION\nSUBSAMPLE\nSIZE",adj=0)
text(2.8,-7.2,expression(n[2]),adj=0, cex=1.1)

arrows(1.8,0.8,8.3,3.9,code=2,lwd=2,angle=15,length=0.2)
arrows(4.8,0.8,9,3.8,code=2,lwd=2,angle=15,length=0.2)
arrows(9.1,0.9,9.5,3.8,code=2,lwd=2,angle=15,length=0.2)
arrows(12.8,0.8,10,3.8,code=2,lwd=2,angle=15,length=0.2)
arrows(2.9,-0.9,2.5,-3.8,code=2,lwd=2,angle=15,length=0.2)
arrows(5.9,-0.9,3.1,-3.8,code=2,lwd=2,angle=15,length=0.2)
arrows(7.4,-0.9,3.5,-3.8,code=2,lwd=2,angle=15,length=0.2)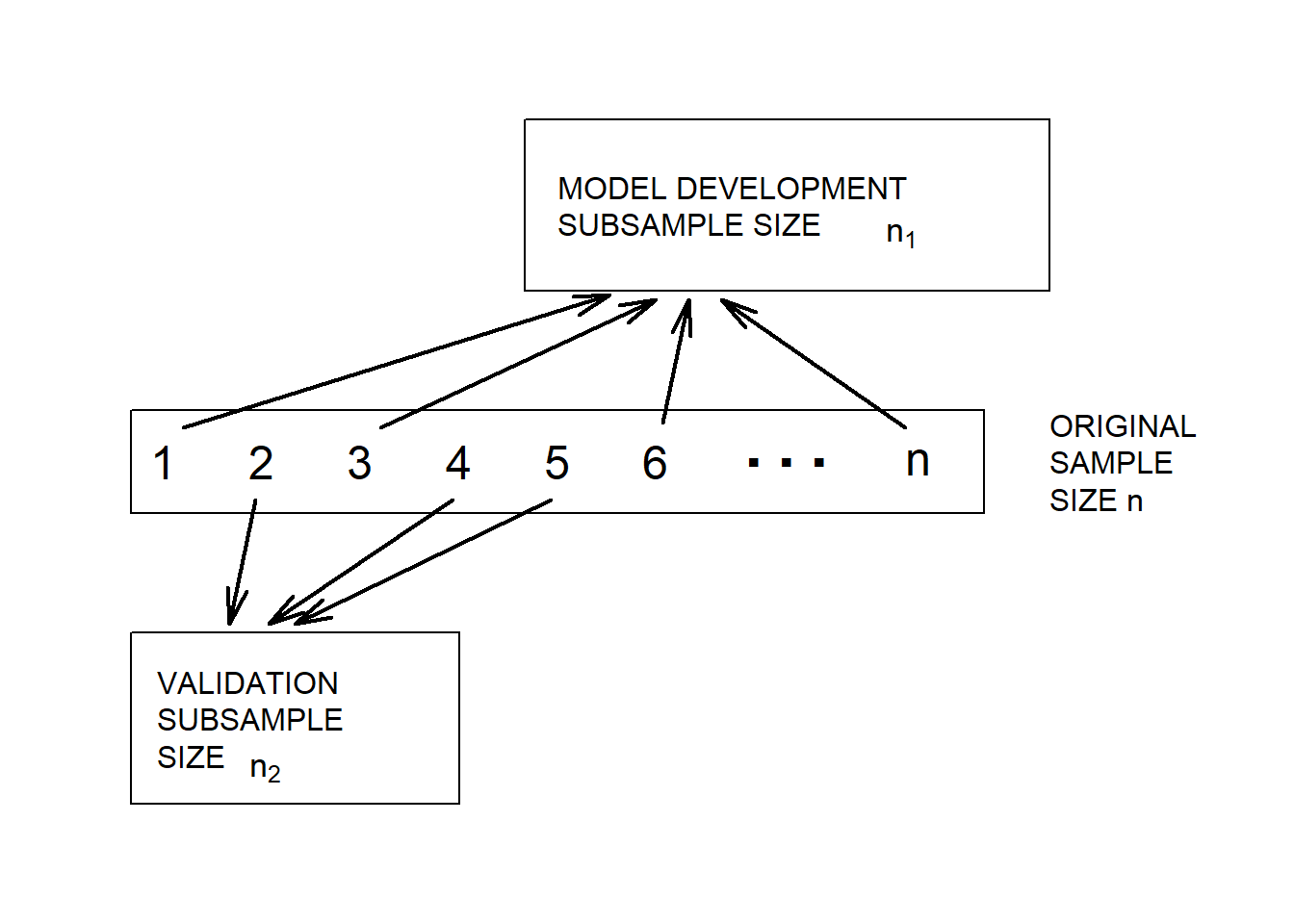

###MC Exercise. An iterative approach to data modeling

Which of the following is not true?

A. Diagnostic checking reveals symptoms of mistakes made in previous specifications.
B. Diagnostic checking provides ways to correct mistakes made in previous specifications.
C. Model formulation is accomplished by using prior knowledge of relationships.
D. Understanding theoretical model properties is not really helpful when matching a model to data or inferring general relationships based on the data.

4.2 Automatic variable selection procedures

In this section, you learn how to:

Identify some examples of automatic variable selection procedures
Describe the purpose of automatic variable selection procedures and their limitations
Describe “data-snooping”

4.2.1 Video

Video Overhead Details

A Details. Classic stepwise regression algorithm

Suppose that the analyst has identified one variable as the outcome, $y$, and $k$ potential explanatory variables, $x_1, x_2, \ldots, x_k$.

(i). Consider all possible regressions using one explanatory variable. Choose the one with the highest t-statistic.
(ii). Add a variable to the model from the previous step. The variable to enter is with the highest t-statistic.
(iii). Delete a variable to the model from the previous step. Delete the variable with the small t-statistic if the statistic is less than, e.g., 2 in absolute value.
(iv). Repeat steps (ii) and (iii) until all possible additions and deletions are performed.

B Details. Drawbacks of stepwise regression

The procedure “snoops” through a large number of models and may fit the data “too well.”
There is no guarantee that the selected model is the best.
- The algorithm does not consider models that are based on nonlinear combinations of explanatory variables.
- It ignores the presence of outliers and high leverage points.

C Details. Data-snooping in stepwise regression

Generate $y$ and $x_1 - x_{50}$ using a random number generator
By design, there is no relation between $y$ and $x_1 - x_{50}$.
But, through stepwise regression, we “discover” a relationship that explains 14% of the variation!!!

Call: lm(formula = y ~ xvar27 + xvar29 + xvar32, data = X)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) -0.04885    0.09531  -0.513   0.6094  
xvar27        0.21063    0.09724   2.166   0.0328 *
xvar29        0.24887    0.10185   2.443   0.0164 *
xvar32        0.25390    0.09823   2.585   0.0112 *

Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9171 on 96 degrees of freedom
Multiple R-squared:  0.1401,    Adjusted R-squared:  0.1132 
F-statistic: 5.212 on 3 and 96 DF,  p-value: 0.002233

D Details. Variants of stepwise regression

This uses the R function step()

The option direction can be used to change how variables enter
- Forward selection. Add one variable at a time without trying to delete variables.
- Backwards selection. Start with the full model and delete one variable at a time without trying to add variables.
The option scope can be used to specify which variables must be included

E Details. Automatic variable selection procedures

Stepwise regression is a type of automatic variable selection procedure.
These procedures are useful because they can quickly search through several candidate models. They mechanize certain routine tasks and are excellent at discovering patterns in data.
They are so good at detecting patterns that they analyst must be wary of overfitting (data-snooping)
They can miss certain patterns (nonlinearities, unusual points)
A model suggested by automatic variable selection procedures should be subject to the same careful diagnostic checking procedures as a model arrived at by any other means

4.2.2 Exercise. Data-snooping in stepwise regression

Assignment Text

Automatic variable selection procedures, such as the classic stepwise regression algorithm, are very good at detecting patterns. Sometimes they are too good in the sense that they detect patterns in the sample that are not evident in the population from which the data are drawn. The detect “spurious” patterns.

This exercise illustrates this phenomenom by using a simulation, designed so that the outcome variable (y) and the explanatory variables are mutually independent. So, by design, there is no relationship between the outcome and the explanatory variables.

As part of the code set-up, we have n = 100 observations generated of the outcome y and 50 explanatory variables, xvar1 through xvar50. As anticipated, collections of explanatory variables are not statistically significant. However, with the step() function, you will find some statistically significant relationships!

Instructions

Fit a basic linear regression model and MLR model with the first ten explanatory variables. Compare the models via an F test.
Fit a multiple linear regression model with all fifty explanatory variables. Compare this model to the one with ten variables via an F test.
Use the step function to find the best model starting with the fitted model containing all fifty explanatory variables and summarize the fit.

Hint. The code shows stepwise regression using BIC, a criterion that results in simpler models than AIC. For AIC, use the option k=2 in the [step()] function (the default)

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6InNldC5zZWVkKDEyMzcpXG5YIDwtIGFzLmRhdGEuZnJhbWUobWF0cml4KHJub3JtKDEwMCo1MCwgbWVhbiA9IDAsIHNkID0gMSksIG5jb2wgPSA1MCkpXG5jb2xuYW1lcyhYKSA8LSBwYXN0ZShcInh2YXJcIiwgMTo1MCwgc2VwID0gXCJcIilcblgkeSA8LSB3aXRoKFgsIG1hdHJpeChybm9ybSgxMDAqMSwgbWVhbiA9IDAsIHNkID0gMSksIG5jb2wgPSAxKSlcbiNjb3IoWFssYyhcInh2YXIxXCIsXCJ4dmFyMlwiLFwieHZhcjNcIixcInh2YXI0XCIsXCJ4dmFyNVwiLFwieHZhcjZcIixcInh2YXI3XCIsXCJ4dmFyOFwiLFwieHZhcjlcIixcInh2YXIxMFwiLFwieVwiKV0sIHVzZSA9IFwiY29tcGxldGUub2JzXCIpIiwic2FtcGxlIjoiIyBGaXQgYSBiYXNpYyBsaW5lYXIgcmVncmVzc2lvbiBtb2RlbCBhbmQgTUxSIG1vZGVsIHdpdGggdGhlIGZpcnN0IHRlbiBleHBsYW5hdG9yeSB2YXJpYWJsZXMuIENvbXBhcmUgdGhlIG1vZGVscyB2aWEgYW4gKkYqIHRlc3QuXG5tb2RlbF9zdGVwMSA8LSBsbSh5IH4geHZhcjEsIGRhdGEgPSBYKVxubW9kZWxfc3RlcDEwIDwtIGxtKHkgfiB4dmFyMSArIHh2YXIyICsgeHZhcjMgKyB4dmFyNCArIHh2YXI1ICsgeHZhcjYgKyB4dmFyNyArIHh2YXI4ICsgeHZhcjkgKyB4dmFyMTAsIGRhdGEgPSBYKVxuYW5vdmEoX19fLCBfX18pXG5cbiMgRml0IGEgbXVsdGlwbGUgbGluZWFyIHJlZ3Jlc3Npb24gbW9kZWwgd2l0aCBhbGwgZmlmdHkgZXhwbGFuYXRvcnkgdmFyaWFibGVzLiBDb21wYXJlIHRoaXMgbW9kZWwgdG8gdGhlIG9uZSB3aXRoIHRlbiB2YXJpYWJsZXMgdmlhIGFuICpGKiB0ZXN0LlxubW9kZWxfc3RlcDUwIDwtIGxtKHkgfiB4dmFyMSArIHh2YXIyICsgeHZhcjMgKyB4dmFyNCArIHh2YXI1ICsgeHZhcjYgKyB4dmFyNyArIHh2YXI4ICsgeHZhcjkgKyB4dmFyMTAgKyB4dmFyMTEgKyB4dmFyMTIgKyB4dmFyMTMgKyB4dmFyMTQgKyB4dmFyMTUgKyB4dmFyMTYgKyB4dmFyMTcgKyB4dmFyMTggKyB4dmFyMTkgKyB4dmFyMjAgKyB4dmFyMjEgKyB4dmFyMjIgKyB4dmFyMjMgKyB4dmFyMjQgKyB4dmFyMjUgKyB4dmFyMjYgKyB4dmFyMjcgKyB4dmFyMjggKyB4dmFyMjkgKyB4dmFyMzAgKyB4dmFyMzEgKyB4dmFyMzIgKyB4dmFyMzMgKyB4dmFyMzQgKyB4dmFyMzUgKyB4dmFyMzYgKyB4dmFyMzcgKyB4dmFyMzggKyB4dmFyMzkgKyB4dmFyNDAgKyB4dmFyNDEgKyB4dmFyNDIgKyB4dmFyNDMgKyB4dmFyNDQgKyB4dmFyNDUgKyB4dmFyNDYgKyB4dmFyNDcgKyB4dmFyNDggKyB4dmFyNDkgKyB4dmFyNTAsIGRhdGEgPSBYKVxuYW5vdmEoX19fLCBfX18pXG5cbiMgVXNlIHRoZSBgc3RlcGAgZnVuY3Rpb24sIHN0YXJ0aW5nIHdpdGggdGhlIGZpdHRlZCBtb2RlbCBjb250YWluaW5nIGFsbCBmaWZ0eSBleHBsYW5hdG9yeSB2YXJpYWJsZXMgYW5kIHN1bW1hcml6ZSB0aGUgZml0LlxuI0ZvciBCSUM6IFxubW9kZWxfc3RlcHdpc2UgPC0gc3RlcChfX18sIGRhdGEgPSBYLCBkaXJlY3Rpb249IFwiYm90aFwiLCBrID0gbG9nKG5yb3coWCkpLCB0cmFjZSA9IDApIFxuc3VtbWFyeShtb2RlbF9zdGVwd2lzZSkiLCJzb2x1dGlvbiI6Im1vZGVsX3N0ZXAxIDwtIGxtKHkgfiB4dmFyMSwgZGF0YSA9IFgpXG5tb2RlbF9zdGVwMTAgPC0gbG0oeSB+IHh2YXIxICsgeHZhcjIgKyB4dmFyMyArIHh2YXI0ICsgeHZhcjUgKyB4dmFyNiArIHh2YXI3ICsgeHZhcjggKyB4dmFyOSArIHh2YXIxMCwgZGF0YSA9IFgpXG5hbm92YShtb2RlbF9zdGVwMSxtb2RlbF9zdGVwMTApXG5tb2RlbF9zdGVwNTAgPC0gbG0oeSB+IHh2YXIxICsgeHZhcjIgKyB4dmFyMyArIHh2YXI0ICsgeHZhcjUgKyB4dmFyNiArIHh2YXI3ICsgeHZhcjggKyB4dmFyOSArIHh2YXIxMCArIHh2YXIxMSArIHh2YXIxMiArIHh2YXIxMyArIHh2YXIxNCArIHh2YXIxNSArIHh2YXIxNiArIHh2YXIxNyArIHh2YXIxOCArIHh2YXIxOSArIHh2YXIyMCArIHh2YXIyMSArIHh2YXIyMiArIHh2YXIyMyArIHh2YXIyNCArIHh2YXIyNSArIHh2YXIyNiArIHh2YXIyNyArIHh2YXIyOCArIHh2YXIyOSArIHh2YXIzMCArIHh2YXIzMSArIHh2YXIzMiArIHh2YXIzMyArIHh2YXIzNCArIHh2YXIzNSArIHh2YXIzNiArIHh2YXIzNyArIHh2YXIzOCArIHh2YXIzOSArIHh2YXI0MCArIHh2YXI0MSArIHh2YXI0MiArIHh2YXI0MyArIHh2YXI0NCArIHh2YXI0NSArIHh2YXI0NiArIHh2YXI0NyArIHh2YXI0OCArIHh2YXI0OSArIHh2YXI1MCwgZGF0YSA9IFgpXG5hbm92YShtb2RlbF9zdGVwMTAsbW9kZWxfc3RlcDUwKVxuXG4jRm9yIEJJQzogXG5tb2RlbF9zdGVwd2lzZSA8LSBzdGVwKG1vZGVsX3N0ZXA1MCwgZGF0YSA9IFgsIGRpcmVjdGlvbj0gXCJib3RoXCIsIGsgPSBsb2cobnJvdyhYKSksIHRyYWNlID0gMCkgXG5zdW1tYXJ5KG1vZGVsX3N0ZXB3aXNlKVxuXG4jIEFuIGV4YW1wbGUgd2l0aCBzY29wZVxuI21vZGVsX3N0ZXA1YSA8LSBzdGVwKG1vZGVsX3N0ZXA0LCBkYXRhID0gWCwgZGlyZWN0aW9uPSBcImJvdGhcIiwgaz1sb2cobnJvdyhYKSksIHRyYWNlID0gMCxcbiAgICAjICAgICAgICAgICAgc2NvcGUgPSBsaXN0KGxvd2VyID0gfnh2YXIxK3h2YXIyLCB1cHBlciA9IG1vZGVsX3N0ZXA0KSkgXG4jc3VtbWFyeShtb2RlbF9zdGVwNWEpXG4jRm9yIEFJQzogXG4jc3RlcChtb2RlbF9zdGVwNCwgZGF0YSA9IFgsIGRpcmVjdGlvbj0gXCJib3RoXCIsIGs9MiwgdHJhY2UgPSAwKSAjIGs9MiBpcyBieSBkZWZhdWx0ICIsInNjdCI6ImV4KCkgJT4lIGNoZWNrX29iamVjdChcIm1vZGVsX3N0ZXAxXCIsIHVuZGVmaW5lZF9tc2c9XCJQbGVhc2UgdXNlIGBsbWAgdG8gY3JlYXRlIGEgbGluZWFyIG1vZGVsLCBhbmQgbmFtZSBpdCBgbW9kZWxfc3RlcDFgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBtb2RlbCBgeWAgdXNpbmcgYHh2YXIxYCBmcm9tIHRoZSBkYXRhZnJhbWUgYHhgLlwiKVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwibW9kZWxfc3RlcDEwXCIsIHVuZGVmaW5lZF9tc2c9XCJQbGVhc2UgdXNlIGBsbWAgdG8gY3JlYXRlIGEgbGluZWFyIG1vZGVsLCBhbmQgbmFtZSBpdCBgbW9kZWxfc3RlcDEwYC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gbW9kZWwgYHlgIHVzaW5nIGB4dmFyYCBmcm9tIDEgdG8gMTAgaW4gdGhlIGRhdGFmcmFtZSBgeGAuXCIpXG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcImFub3ZhXCIsIGluZGV4PTEsIG5vdF9jYWxsZWRfbXNnPVwiVXNlIGBhbm92YWAgdG8gY29tcGFyZSB0aGUgdHdvIGxpbmVhciBtb2RlbHMgd2UgaGF2ZSBqdXN0IGNyZWF0ZWQuXCIpICU+JSBjaGVja19yZXN1bHQoKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBjb21wYXJlIGBtb2RlbF9TdGVwMWAgdG8gYG1vZGVsX3N0ZXAxMGAuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJtb2RlbF9zdGVwNTBcIiwgdW5kZWZpbmVkX21zZz1cIlBsZWFzZSB1c2UgYGxtYCB0byBjcmVhdGUgYSBsaW5lYXIgbW9kZWwsIGFuZCBuYW1lIGl0IGBtb2RlbF9zdGVwNTBgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBtb2RlbCBgeWAgdXNpbmcgYWxsIDUwIGB4dmFyYHMgZnJvbSB0aGUgZGF0YWZyYW1lIGB4YC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwiYW5vdmFcIiwgaW5kZXg9Miwgbm90X2NhbGxlZF9tc2c9XCJVc2UgYGFub3ZhYCB0byBjb21wYXJlIHRoZSB0d28gbW9zdCByZWNlbnQgbGluZWFyIG1vZGVscy5cIikgJT4lIGNoZWNrX3Jlc3VsdCgpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIGNvbXBhcmUgYG1vZGVsX3N0ZXAxMGAgd2l0aCBgbW9kZWxfc3RlcDUwYC5cIilcbmV4KCkgJT4lIGNoZWNrX29iamVjdChcIm1vZGVsX3N0ZXB3aXNlXCIsIHVuZGVmaW5lZF9tc2c9XCJNYWtlIHN1cmUgdG8gdXNlIHRoZSBgc3RlcGAgZnVuY3Rpb24gdG8gdHJhbnNmb3JtIGBtb2RlbF9zdGVwNTBgIGludG8gYSBtb3JlIHVzZWZ1bCBtb2RlbCwgbmFtZWQgYG1vZGVsX3N0ZXB3aXNlYC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc3BlY2lmeSB0aGF0IHdlIHdhbnQgdG8gZWRpdCBgbW9kZWxfc3RlcDUwYCwgdXNpbmcgdGhlIGRhdGEgZm91bmQgaW4gYHhgIGluIGBib3RoYCBkaXJlY3Rpb25zLCBhIHRyYWNlIHZhbHVlIG9mIGAwYCBhbmQgayBzZXQgdG8gdGhlIGxvZyBvZiB0aGUgbnVtYmVyIG9mIHJvd3MgaW4gYHhgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsIG5vdF9jYWxsZWRfbXNnPVwiVXNlIGBzdW1tYXJ5YCB0byB0YWtlIGEgbG9vayBhdCBgbW9kZWxfc3RlcHdpc2VgLlwiKSAlPiUgY2hlY2tfYXJnKC4sIFwib2JqZWN0XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIGNhbGwgYHN1bW1hcnlgIG9uIGBtb2RlbF9zdGVwd2lzZWAuXCIpXG5zdWNjZXNzX21zZyhcIkV4Y2VsbGVudCEgVGhlIHN0ZXAgcHJvY2VkdXJlIHJlcGVhdGVkbHkgZml0cyBtYW55IG1vZGVscyB0byBhIGRhdGEgc2V0LiBXZSBzdW1tYXJpemUgZWFjaCBmaXQgd2l0aCBoeXBvdGhlc2lzIHRlc3Rpbmcgc3RhdGlzdGljcyBsaWtlIHQtc3RhdGlzdGljcyBhbmQgcC12YWx1ZXMuIEJ1dCwgcmVtZW1iZXIgdGhhdCBoeXBvdGhlc2lzIHRlc3RzIGFyZSBkZXNpZ25lZCB0byBmYWxzZWx5IGRldGVjdCBhIHJlbGF0aW9uc2hpcCBhIGZyYWN0aW9uIG9mIHRoZSB0aW1lICh0eXBpY2FsbHkgNSUpLiBGb3IgZXhhbXBsZSwgaWYgeW91IHJ1biBhIHQtdGVzdCA1MCB0aW1lcyAoZm9yIGVhY2ggZXhwbGFuYXRvcnkgdmFyaWFibGUpLCB5b3UgY2FuIGV4cGVjdCB0byBnZXQgdHdvIG9yIHRocmVlIHN0YXRpc3RpY2FsbHkgc2lnbmlmaWNhbnQgZXhwbGFuYXRvcnkgdmFyaWFibGVzIGV2ZW4gZm9yIHVucmVsYXRlZCB2YXJpYWJsZXMgKGJlY2F1c2UgNTAgdGltZXMgMC4wNSA9IDIuNSkuXCIpIiwiaGludCI6IlRoZSA8Y29kZT5zdGVwKCk8L2NvZGU+IGZ1bmN0aW9uIGF1dG9tYXRpY2FsbHkgc2VsZWN0cyB3aGljaCBleHBsYW5hdG9yeSB2YXJpYWJsZXMgYXJlIHNpZ25pZmljYW50IGVub3VnaCB0byBiZWxvbmcgaW4gdGhlIG1vZGVsIGdpdmVuIGEgZ29vZG5lc3Mgb2YgZml0IGNyaXRlcmlvbi4gSGF2aW5nIGs9bG9nKG5yb3coeCkpIHNwZWNpZmllcyB1c2luZyBCSUMuIn0=

4.3 Residual analysis

In this section, you learn how to:

Explain how residual analysis can be used to improve a model specification
Use relationships between residuals and potential explanatory variables to improve model specification

4.3.1 Video

Video Overhead Details

A Details. Residual analysis

Use $e_i = y_i - \hat{y}_i$ as the ith residual.
Later, I will discuss rescaling by, for example, $s$, to get a standardized residual.
Role of residuals: If the model formulation is correct, then residuals should be approximately equal to random errors or “white noise.”
Method of attack: Look for patterns in the residuals. Use this information to improve the model specification.

B Details. Using residuals to select explanatory variables

Residual analysis can help identify additional explanatory variables that may be used to improve the formulation of the model.
If the model is correct, then residuals should resemble random errors and contain no discernible patterns.
Thus, when comparing residuals to explanatory variables, we do not expect any relationships.
If we do detect a relationship, then this suggests the need to control for this additional variable.

C Details. Detecting relationships between residuals and explanatory variables

Calculate summary statistics and display the distribution of residuals to identify outliers.
Calculate the correlation between the residuals and additional explanatory variables to search for linear relationships.
Create scatter plots between the residuals and additional explanatory variables to search for nonlinear relationships.

4.3.2 Exercise. Residual analysis and risk manager survey

Assignment Text

This exercise examines data, pre-loaded in the dataframe survey, from a survey on the cost effectiveness of risk management practices. Risk management practices are activities undertaken by a firm to minimize the potential cost of future losses, such as the event of a fire in a warehouse or an accident that injures employees. This exercise develops a model that can be used to make statements about cost of managing risks.

A measure of risk management cost effectiveness, logcost, is the outcome variable. This variable is defined as total property and casualty premiums and uninsured losses as a proportion of total assets, in logarithmic units. It is a proxy for annual expenditures associated with insurable events, standardized by company size. Explanatory variables include logsize, the logarithm of total firm assets, and indcost, a measure of the firm’s industry risk.

Instructions

Fit and summarize a MLR model using logcost as the outcome variable and logsize and indcost as explanatory variables.
Plot residuals of the fitted model versus indcost and superimpose a locally fitted line using the R function lowess().
Fit and summarize a MLR model of logcost on logsize, indcost and a squared version of indcost.
Plot residuals of the fitted model versus `indcost’ and superimpose a locally fitted line using lowess().

Hint. You can access model residuals using mlr.survey1$residuals or mlr.survey1($residuals)

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNzdXJ2ZXkgPC0gcmVhZC5jc3YoXCJDU1ZEYXRhXFxcXFJpc2tfc3VydmV5LmNzdlwiLCBoZWFkZXI9VFJVRSlcbnN1cnZleSA8LSByZWFkLmNzdihcImh0dHBzOi8vYXNzZXRzLmRhdGFjYW1wLmNvbS9wcm9kdWN0aW9uL3JlcG9zaXRvcmllcy8yNjEwL2RhdGFzZXRzL2RjMWM1YmNlNDNlZjA3NmFhNzcxNjlhMjQyMTE4ZTJlNThkMDFmODIvUmlza19zdXJ2ZXkuY3N2XCIsIGhlYWRlcj1UUlVFKVxuc3VydmV5JGxvZ2Nvc3QgPC0gbG9nKHN1cnZleSRmaXJtY29zdClcbiNzdHIoc3VydmV5KSIsInNhbXBsZSI6IiMgUmVncmVzcyBgbG9nY29zdGAgb24gYGxvZ3NpemVgIGFuZCBgaW5kY29zdGAgXG5tbHIuc3VydmV5MSA8LSBsbShsb2djb3N0IH4gbG9nc2l6ZSArIGluZGNvc3QsIGRhdGEgPSBzdXJ2ZXkpXG5zdW1tYXJ5KF9fXylcblxuIyBQbG90IHJlc2lkdWFscyBvZiB0aGUgZml0dGVkIG1vZGVsIHZlcnN1cyBgaW5kY29zdGAgYW5kIHN1cGVyaW1wb3NlIGEgbG9jYWxseSBmaXR0ZWQgbGluZSB1c2luZyB0aGUgIGZ1bmN0aW9uIFtsb3dlc3MoKV1cbnBsb3Qoc3VydmV5JGluZGNvc3QsICBfX18pXG5saW5lcyhsb3dlc3Moc3VydmV5JGluZGNvc3QsIF9fXykpXG5cbiMgUmVncmVzcyBgbG9nY29zdGAgb24gYGxvZ3NpemVgIGFuZCBgaW5kY29zdGAgYW5kIGBpbmRjb3N0YCBzcXVhcmVkXG5tbHIuc3VydmV5MiA8LSBsbShfX18gfiBsb2dzaXplICsgcG9seShpbmRjb3N0LDIpLCBkYXRhID0gc3VydmV5KVxuc3VtbWFyeShfX18pXG5cbiMgUGxvdCByZXNpZHVhbHMgb2YgdGhpcyBmaXR0ZWQgbW9kZWwgYW5kIHN1cGVyaW1wb3NlIGEgbG9jYWxseSBmaXR0ZWQgbGluZSB1c2luZyB0aGUgZnVuY3Rpb24gW2xvd2VzcygpXVxucGxvdChzdXJ2ZXkkaW5kY29zdCwgX19fKVxubGluZXMobG93ZXNzKHN1cnZleSRpbmRjb3N0LCBfX18pKSIsInNvbHV0aW9uIjoibWxyLnN1cnZleTEgPC0gbG0obG9nY29zdCB+IGxvZ3NpemUgKyBpbmRjb3N0LCBkYXRhID0gc3VydmV5KVxuc3VtbWFyeShtbHIuc3VydmV5MSlcblxucGxvdChzdXJ2ZXkkaW5kY29zdCwgbWxyLnN1cnZleTEkcmVzaWR1YWxzKVxubGluZXMobG93ZXNzKHN1cnZleSRpbmRjb3N0LG1sci5zdXJ2ZXkxJHJlc2lkdWFscykpXG5cbm1sci5zdXJ2ZXkyIDwtIGxtKGxvZ2Nvc3QgfiBsb2dzaXplICsgcG9seShpbmRjb3N0LDIpLCBkYXRhID0gc3VydmV5KVxuc3VtbWFyeShtbHIuc3VydmV5MilcblxucGxvdChzdXJ2ZXkkaW5kY29zdCwgbWxyLnN1cnZleTIkcmVzaWR1YWxzKVxubGluZXMobG93ZXNzKHN1cnZleSRpbmRjb3N0LG1sci5zdXJ2ZXkyJHJlc2lkdWFscykpIiwic2N0IjoiZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwibWxyLnN1cnZleTFcIiwgdW5kZWZpbmVkX21zZz1cIlVzZSBgbG1gIHRvIGNyZWF0ZSBhIGxpbmVhciBtb2RlbCBuYW1lZCBgbWxyLnN1cnZleTFgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIm1ha2Ugc3VyZSB0byBtb2RlbCBgbG9nY29zdGAgdXNpbmcgYGxvZ3NpemVgIGFuZCBgaW5kY29zdGAgZnJvbSB0aGUgZGF0YWZyYW1lIGBzdXJ2ZXlgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsaW5kZXg9MSwgbm90X2NhbGxlZF9tc2c9XCJVc2UgdGhlIGBzdW1tYXJ5YCBmdW5jdGlvbiB0byB2aWV3IHRoZSBzdW1tYXJ5IHN0YXRzIG9mIGBtbHIuc3VydmV5MWAuXCIpICU+JSBjaGVja19hcmcoLiwgXCJvYmplY3RcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc3BlY2lmeSB0aGF0IHdlIHdvdWxkIGxpa2UgdGhlIHN1bW1hcnkgc3RhdHMgb2YgYG1sci5zdXJ2ZXkxYC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwicGxvdFwiLCBpbmRleD0xLCBub3RfY2FsbGVkX21zZz1cInBsZWFzZSBjcmVhdGUgYSBwbG90IHRoYXQgc2hvd3MgdGhlIHJlc2lkdWFscyBvZiBgaW5kY29zdHNgIGFuZCBgbWxyLnN1cnZleTFgXCIpICU+JXtcbiAgY2hlY2tfYXJnKC4sIFwieFwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoZSBpbmRlcGVuZGVudCB2YXJpYWJsZSBzaG91bGQgYmUgYGluZGNvc3RzYC5cIilcbiAgY2hlY2tfYXJnKC4sIFwieVwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoZSBkZXBlbmRlbnQgdmFyaWFibGUgc2hvdWxkIGJlIHRoZSByZXNpZHVhbHMgb2YgYG1sci5zdXJ2ZXkxYC5cIilcbn1cbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwibGluZXNcIiwgaW5kZXg9MSwgbm90X2NhbGxlZF9tc2c9XCJQbGVhc2UgdXNlIHRoZSBgbGluZXNgIGZ1bmN0aW9uIHRvIGFkZCBhIGxpbmUgdG8gdGhlIHBsb3QuIFwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJsb3dlc3NcIiwgaW5kZXg9MSwgbm90X2NhbGxlZF9tc2c9XCJQbGVhc2UgdXNlIHRoZSBgbG93ZXNzYCBmdW5jdGlvbiB0byBhZGQgYSBzbW9vdGhlZCBlZmZlY3Qgb24gb3VyIGxpbmUuXCIpICU+JXtcbiAgY2hlY2tfYXJnKC4sIFwieFwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoZSBmaXJzdCBhcmd1bWVudCBzaG91bGQgYmUgYGluZGNvc3RzYC5cIilcbiAgY2hlY2tfYXJnKC4sIFwieVwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoZSBzZWNvbmQgYXJndW1lbnQgc2hvdWxkIGJlIHRoZSByZXNpZHVhbHMgZnJvbSBgbWxyLnN1cnZleTFgLlwiKVxufVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwibWxyLnN1cnZleTJcIiwgdW5kZWZpbmVkX21zZz1cIlVzZSBgbG1gIHRvIGNyZWF0ZSBhIGxpbmVhciBtb2RlbCB0aGF0IGlzIHN0b3JlZCB1bmRlciB0aGUgbmFtZSBgbWxyLnN1cnZleTJgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBtb2RlbCBgbG9nY29zdGAgdXNpbmcgYGxvZ3NpemVgIGFuZCBgaW5kY29zdGAgc3F1YXJlZCwgd2hpY2ggY2FuIGJlIGZvdW5kIHVzaW5nIGBwb2x5KGluZGNvc3QsMilgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsIGluZGV4PTIsIG5vdF9jYWxsZWRfbXNnPVwiVXNlIGBzdW1tYXJ5YCB0byB0YWtlIGEgbG9vayBhdCBgbWxyLnN1cnZleTJgLlwiKSAlPiUgY2hlY2tfYXJnKC4sIFwib2JqZWN0XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIHNwZWNpZnkgdGhhdCB3ZSB3YW50IGEgc3VtbWFyeSBvZiBgbWxyLnN1cnZleTJgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJwbG90XCIsIGluZGV4PTIsIG5vdF9jYWxsZWRfbXNnPVwiTm93IG1ha2UgYSBwbG90IHRoYXQgc2hvd3MgdGhlIGBpbmRjb3N0YCBiYXNlZCBvbiB0aGUgcmVzaWR1YWxzIG9mIGBtbHIuc3VydmV5MmAuXCIpICU+JXtcbiAgY2hlY2tfYXJnKC4sIFwieFwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRoZSBpbmRlcGVuZGVudCB2YXJpYWJsZSBzaG91bGQgYmUgYGluZGNvc3RgLlwiKVxuICBjaGVja19hcmcoLiwgXCJ5XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhlIGRlcGVuZGVudCB2YXJpYWJsZSBzaG91bGQgYmUgdGhlIHJlc2lkdWFscyBvZiBgbWxyLnN1cnZleTJgLlwiKVxufVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJsaW5lc1wiLCBpbmRleD0yLCBub3RfY2FsbGVkX21zZz1cIk1ha2Ugc3VyZSB0byBhZGQgYSBsaW5lIHRvIHRoaXMgbmV3IGdyYXBoIHVzaW5nIGBsaW5lc2AuXCIpXG5cbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwibG93ZXNzXCIsIGluZGV4PTIsIG5vdF9jYWxsZWRfbXNnPVwibWFrZSBzdXJlIHRvIHVzZSB0aGUgYGxvd2Vzc2AgZnVuY3Rpb24gdG8gYWRkIGEgc21vb3RoZWQgZWZmZWN0IHRvIHRoZSBsaW5lLiBcIikgJT4le1xuICBjaGVja19hcmcoLiwgXCJ4XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhlIGZpcnN0IGFyZ3VtZW50IHNob3VsZCBiZSBgaW5kY29zdGAuXCIpXG4gIGNoZWNrX2FyZyguLCBcInlcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJUaGUgc2Vjb25kIGFyZ3VtZW50IHNob3VsZCBiZSB0aGUgcmVzaWR1YWxzIG9mIGBtbHIuc3VydmV5MmAuXCIpXG59XG5zdWNjZXNzX21zZyhcIkV4Y2VsbGVudCEgSW4gdGhpcyBleGVyY2lzZSwgeW91IGV4YW1pbmVkIHJlc2lkdWFscyBmcm9tIGEgcHJlbGltaW5hcnkgbW9kZWwgZml0IGFuZCBkZXRlY3RlZCBhIG1pbGQgcXVhZHJhdGljIHBhdHRlcm4gaW4gYSB2YXJpYWJsZS4gVGhpcyBzdWdnZXN0ZWQgZW50ZXJpbmcgdGhlIHNxdWFyZWQgdGVybSBvZiB0aGF0IHZhcmlhYmxlIGludG8gdGhlIG1vZGVsIHNwZWNpZmljYXRpb24uIFRoZSByZWZpdCBvZiB0aGlzIG5ldyBtb2RlbCBzdWdnZXN0cyB0aGF0IHRoZSBzcXVhcmVkIHRlcm0gaGFzIGltcG9ydGFudCBleHBsYW5hdG9yeSBpbmZvcm1hdGlvbi4gVGhlIHNxdWFyZWQgdGVybSBpcyBhIG5vbmxpbmVhciBhbHRlcm5hdGl2ZSB0aGF0IGlzIG5vdCBhdmFpbGFibGUgaW4gbWFueSBhdXRvbWF0aWMgdmFyaWFibGUgc2VsZWN0aW9uIHByb2NlZHVyZXMuXCIpIiwiaGludCI6IlRoZSBiZXN0IHdheSB0byB1dGlsaXplIHRoZSByZXNpZHVhbHMgZnJvbSBhIGxpbmVhciBtb2RlbCBpcyA8Y29kZT5tb2RlbC5uYW1lJHJlc2lkdWFsczwvY29kZT4uIn0=

4.3.3 Exercise. Added variable plot and refrigerator prices

Assignment Text

What characteristics of a refrigerator are important in determining its price (price)? We consider here several characteristics of a refrigerator, including the size of the refrigerator in cubic feet (rsize), the size of the freezer compartment in cubic feet (fsize), the average amount of money spent per year to operate the refrigerator (ecost, for energy cost), the number of shelves in the refrigerator and freezer doors (shelves), and the number of features (features). The features variable includes shelves for cans, see-through crispers, ice makers, egg racks and so on.

Both consumers and manufacturers are interested in models of refrigerator prices. Other things equal, consumers generally prefer larger refrigerators with lower energy costs that have more features. Due to forces of supply and demand, we would expect consumers to pay more for these refrigerators. A larger refrigerator with lower energy costs that has more features at the similar price is considered a bargain to the consumer. How much extra would the consumer be willing to pay for this additional space? A model of prices for refrigerators on the market provides some insight to this question.

To this end, we analyze data from n = 37 refrigerators.

Instructions

# Pre-exercise code
Refrig <- read.table("CSVData\\Refrig.csv", header = TRUE, sep = ",")
summary(Refrig)
Refrig1 <- Refrig[c("price", "ecost", "rsize", "fsize", "shelves", "s_sq_ft", "features")]
round(cor(Refrig1), digits = 3)
refrig_mlr1 <- lm(price ~ rsize + fsize + shelves + features, data = Refrig)
summary(refrig_mlr1)
Refrig$residuals1 <- residuals(refrig_mlr1)
refrig_mlr2 <- lm(ecost ~ rsize + fsize + shelves + features, data = Refrig)
summary(refrig_mlr2)
Refrig$residuals2 <- residuals(refrig_mlr2)
plot(Refrig$residuals2, Refrig$residuals1)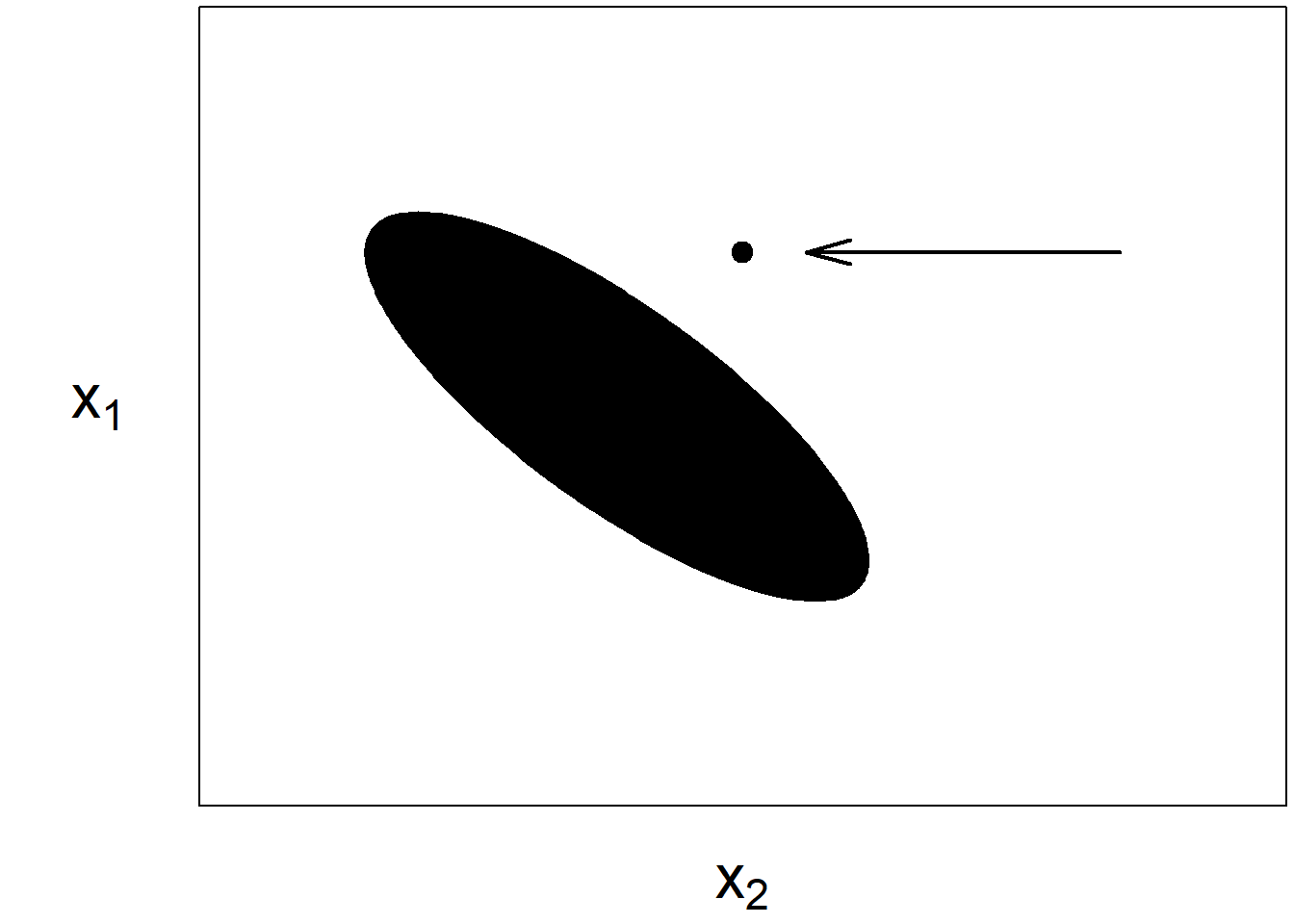

#library(Rcmdr)
#refrig_mlr3 <- lm(price ~ rsize + fsize + shelves + features + ecost, data = Refrig)
#avPlots(refrig_mlr3, terms = "ecost")

     price            ecost           rsize          fsize      
 Min.   : 460.0   Min.   :60.00   Min.   :12.6   Min.   :4.100  
 1st Qu.: 545.0   1st Qu.:66.00   1st Qu.:12.9   1st Qu.:4.400  
 Median : 590.0   Median :68.00   Median :13.2   Median :5.100  
 Mean   : 626.4   Mean   :70.51   Mean   :13.4   Mean   :5.184  
 3rd Qu.: 685.0   3rd Qu.:75.00   3rd Qu.:13.9   3rd Qu.:5.700  
 Max.   :1200.0   Max.   :94.00   Max.   :14.7   Max.   :7.400  
    shelves         s_sq_ft         features     
 Min.   :1.000   Min.   :20.60   Min.   : 1.000  
 1st Qu.:2.000   1st Qu.:23.40   1st Qu.: 2.000  
 Median :2.000   Median :24.00   Median : 3.000  
 Mean   :2.514   Mean   :24.53   Mean   : 3.459  
 3rd Qu.:3.000   3rd Qu.:25.50   3rd Qu.: 5.000  
 Max.   :5.000   Max.   :30.20   Max.   :12.000  
          price  ecost  rsize  fsize shelves s_sq_ft features
price     1.000  0.522 -0.024  0.720   0.400   0.155    0.697
ecost     0.522  1.000 -0.033  0.855   0.188   0.058    0.334
rsize    -0.024 -0.033  1.000 -0.235  -0.363   0.401   -0.096
fsize     0.720  0.855 -0.235  1.000   0.251   0.110    0.439
shelves   0.400  0.188 -0.363  0.251   1.000  -0.527    0.160
s_sq_ft   0.155  0.058  0.401  0.110  -0.527   1.000    0.083
features  0.697  0.334 -0.096  0.439   0.160   0.083    1.000

Call:
lm(formula = price ~ rsize + fsize + shelves + features, data = Refrig)

Residuals:
     Min       1Q   Median       3Q      Max 
-128.200  -34.963    7.081   28.716  155.096 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -698.89     302.60  -2.310  0.02752 *  
rsize          56.50      20.56   2.748  0.00977 ** 
fsize          75.40      13.93   5.414 5.96e-06 ***
shelves        35.92      11.08   3.243  0.00277 ** 
features       25.16       5.04   4.992 2.04e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 68.11 on 32 degrees of freedom
Multiple R-squared:  0.789, Adjusted R-squared:  0.7626 
F-statistic: 29.92 on 4 and 32 DF,  p-value: 2.102e-10


Call:
lm(formula = ecost ~ rsize + fsize + shelves + features, data = Refrig)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.8483 -4.3064  0.5154  2.6324  9.3596 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -14.2165    20.9365  -0.679   0.5020    
rsize         2.8744     1.4225   2.021   0.0517 .  
fsize         8.9085     0.9636   9.245 1.49e-10 ***
shelves       0.2895     0.7664   0.378   0.7081    
features     -0.2006     0.3487  -0.575   0.5692    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.712 on 32 degrees of freedom
Multiple R-squared:  0.7637,    Adjusted R-squared:  0.7342 
F-statistic: 25.86 on 4 and 32 DF,  p-value: 1.247e-09

4.4 Unusual observations

In this section, you learn how to:

Compare and contrast three alternative definitions of a standardized residual
Evaluate three alternative options for dealing with outliers
Assess the impact of a high leverage observation
Evaluate options for dealing with high leverage observations
Describe the notion of influence and Cook’s Distance for quantifying influence

4.4.1 Video

Video Overhead Details

A Details. Unusual observations

Regression coefficients can be expressed as (matrix) weighted averages of outcomes
- Averages, even weighted averages can be strongly influenced by unusual observations
Observations may be unusual in the y direction or in the X space
For unusual in the y direction, we use a residual $e = y - \hat{y}$
- By subtracting the fitted value $\hat{y}$, we look to the y distance from the regression plane
- In this way, we “control” for values of explanatory variables

B Details. Standardized residuals

We standardize residuals so that we can focus on relationships of interest and achieve carry-over of experience from one data set to another.

Three commonly used definitions of standardize residuals are:

\[ \text{(a) }\frac{e_i}{s}, \ \ \ \text{ (b) }\frac{e_i}{s\sqrt{1-h_{ii}}}, \ \ \ \text{(c)}\frac{e_i}{s_{(i)}\sqrt{1-h_{ii}}}. \]

First choice is simple
Second choice, from theory, $\mathrm{Var}(e_i)=\sigma ^{2}(1-h_{ii}).$ Here, $h_{ii}$ is the $i$th leverage (defined later).
Third choice is termed “studentized residuals”. Idea: numerator is independent of the denominator.

C Details. Outlier - an unusal standardized residual

An outlier is an observation that is not well fit by the model; these are observations where the residual is unusually large.
Unusual means what? Many packages mark a point if the |standardized residual| > 2.
Options for handling outliers
- Ignore them in the analysis but be sure to discuss their effects.
- Delete them from the data set (but be sure to discuss their effects).
- Create a binary variable to indicator their presence. (This will increase your $R^2$!)

D Details. High leverage points

A high leverage point is an observation that is “far away” in the $x$-space from others.
One can get a feel for high leverage observations by looking a summary statistics (mins, maxs) for each explanatory variable.
Options for dealing with high leverage points are comparable to outliers, we can ignore their effects, delete them, or mark them with a binary indicator variable.

E Details. High leverage point graph

library(cluster)
#library(MASS)
par(mar=c(3.2,5.4,.2,.2))
plot(1,5,type="p",pch=19,cex=1.5,xlab="",ylab="",cex.lab=1.5,xaxt="n",yaxt="n",xlim=c(-3,5),ylim=c(-12,12))
mtext(expression(x[2]), side=1,line=2, cex=2.0)
mtext(expression(x[1]), side=2, line=2, las=2, cex=2.0)
arrows(1.5,5,4,5,code=1,lwd=2,angle=15,length=0.25)
xycov<-matrix(c(2, -5,-5, 20),nrow=2,ncol=2)
xyloc<-matrix(c(0, 0),nrow=1,ncol=2)
polygon(ellipsoidPoints(xycov, d2 = 2, loc=xyloc),col="black")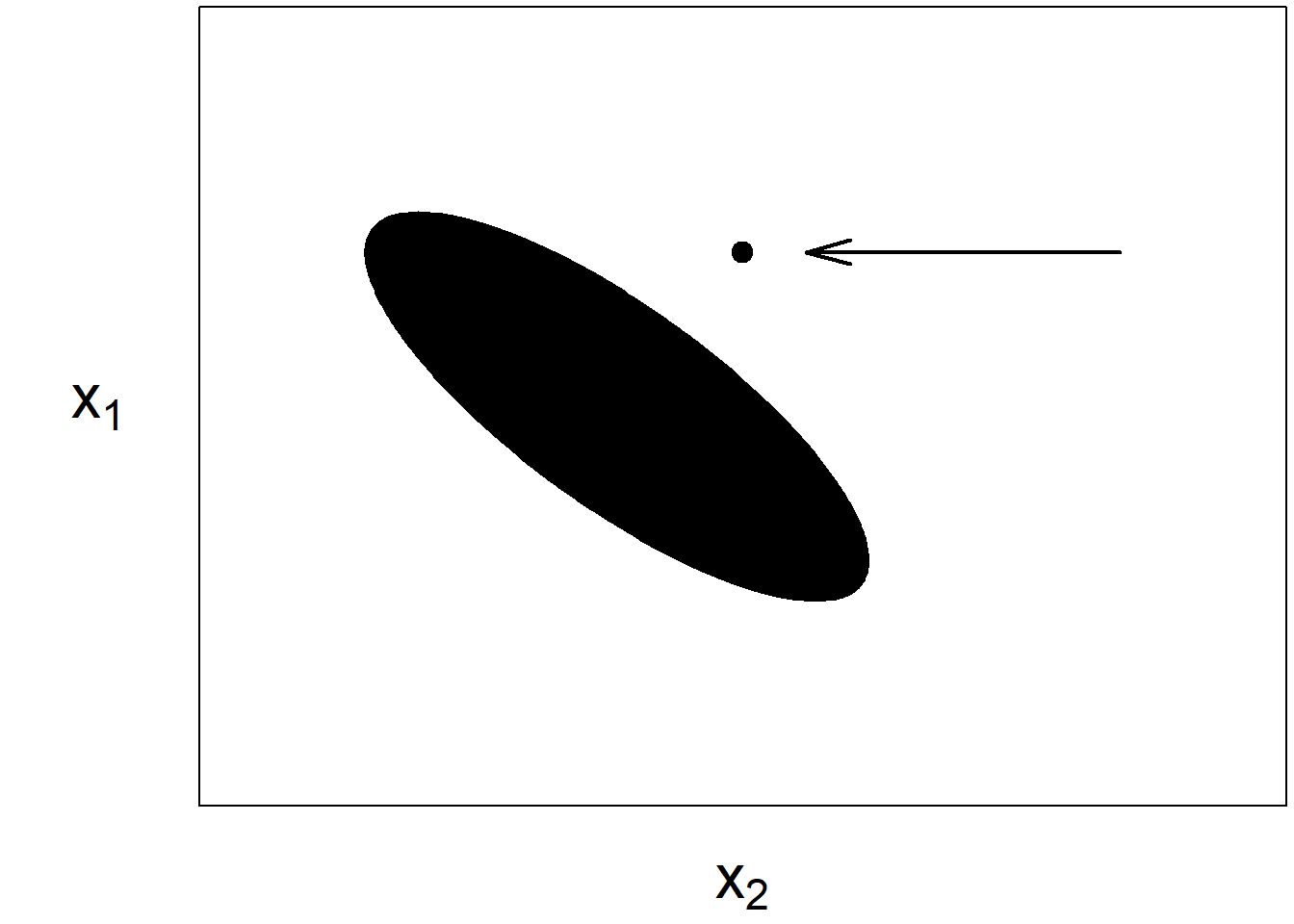

F Details. Leverage

Using matrix algebra, one can express the ith fitted value as a linear combination of observations

\[ \hat{y}_{i} = h_{i1} y_{1} + \cdots +h_{ii}y_{i}+\cdots+h_{in}y_{n}. \]

The term $h_{ii}$ is known as the ith leverage
- The larger the value of $h_{ii}$, the greater the effect of the ith observation $y_i$ on the ith fitted value $\hat{y}_i$.
- Statistical routines have values of the leverage coded, so computing this quantity. The key thing to know is that $h_{ii}$ is based solely on the explanatory variables. If you change the $y$ values, the leverage does not change.
- As a commonly used rule of thumb, a leverage is deemed to be “unusual” if its value exceeds three times the average (= number of regression coefficients divided by the number of observations.)

4.4.2 Exercise. Outlier example

In chapter 2, we consider a fictitious data set of 19 “base” points plus three different types of unusual points. In this exercise, we consider the effect of one unusal point, “C”, this both an outlier (unusual in the “y” direction) and a high leverage point (usual in the x-space). The data have been pre-loaded in the dataframe outlrC.

Instructions

Fit a basic linear regression model of y on x and store the result in an object.
Use the function rstandard() to extract the standardized residuals from the fitted regression model object and summarize them.
Use the function hatvalues() to extract the leverages from the model fitted and summarize them.
Plot the standardized residuals versus the leverages to see the relationship between these two measures that calibrate how unusual an observation is.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNvdXRsciA8LSByZWFkLmNzdihcIkNTVkRhdGFcXFxcT3V0bGllci5jc3ZcIiwgaGVhZGVyID0gVFJVRSlcbm91dGxyIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvN2EzODkxMmU1NDRjMzFmYzZmNWZjYTEyYjlhMmViNjQ1ZjJiY2QzMi9PdXRsaWVyLmNzdlwiLCBoZWFkZXIgPSBUUlVFKVxub3V0bHJDIDwtIG91dGxyWy1jKDIwLDIxKSxjKFwieFwiLFwieVwiKV0iLCJzYW1wbGUiOiJvdXRsckMgPC0gb3V0bHJbLWMoMjAsMjEpLGMoXCJ4XCIsXCJ5XCIpXVxuXG4jIEZpdCBhIGJhc2ljIGxpbmVhciByZWdyZXNzaW9uIG1vZGVsIG9mIGB5YCBvbiBgeGAgYW5kIHN0b3JlIHRoZSByZXN1bHQgaW4gYW4gb2JqZWN0LlxubW9kZWxfb3V0bHJDIDwtIGxtKHkgfiB4LCBkYXRhID0gb3V0bHJDKVxuXG4jIEV4dHJhY3QgdGhlIHN0YW5kYXJkaXplZCByZXNpZHVhbHMgZnJvbSB0aGUgZml0dGVkIHJlZ3Jlc3Npb24gbW9kZWwgb2JqZWN0IGFuZCBzdW1tYXJpemUgdGhlbS5cbnJpIDwtIHJzdGFuZGFyZChtb2RlbF9vdXRsckMpXG5zdW1tYXJ5KHJpKVxuXG4jIEV4dHJhY3QgdGhlIGxldmVyYWdlcyBmcm9tIHRoZSBtb2RlbCBmaXR0ZWQgYW5kIHN1bW1hcml6ZSB0aGVtLiBcbmhpaSA8LSBoYXR2YWx1ZXMobW9kZWxfb3V0bHJDKVxuc3VtbWFyeShoaWkpXG5cbiMgUGxvdCB0aGUgc3RhbmRhcmRpemVkIHJlc2lkdWFscyB2ZXJzdXMgdGhlIGxldmVyYWdlc1xucGxvdChoaWkscmkpIiwic29sdXRpb24iOiJwbG90KG91dGxyQylcbm1vZGVsX291dGxyQyA8LSBsbSh5IH4geCwgZGF0YSA9IG91dGxyQylcbnJpIDwtIHJzdGFuZGFyZChtb2RlbF9vdXRsckMpXG5zdW1tYXJ5KHJpKVxuaGlpIDwtIGhhdHZhbHVlcyhtb2RlbF9vdXRsckMpXG5zdW1tYXJ5KGhpaSlcbnBsb3QoaGlpLHJpKSIsInNjdCI6ImV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwicGxvdFwiLGluZGV4PTEsIG5vdF9jYWxsZWRfbXNnPVwiUGxlYXNlIHVzZSBgcGxvdGAgdG8gY3JlYXRlIGEgcGxvdCBvZiB0aGUgZGF0YSBpbiBgb3V0bHJDYC5cIikgJT4lIGNoZWNrX2FyZyguLCBcInhcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc3BlY2lmeSB0aGF0IHdlIHdhbnQgdG8gcGxvdCB0aGUgZGF0YSBmb3VuZCBpbiBgb3V0bHJDYC5cIilcbmV4KCkgJT4lIGNoZWNrX29iamVjdChcIm1vZGVsX291dGxyQ1wiLCB1bmRlZmluZWRfbXNnPVwiTWFrZSBzdXJlIHRvIGNyZWF0ZSBhIGxpbmVhciBtb2RlbCBhbmQgc3RvcmUgaXQgdW5kZXIgdGhlIG5hbWUgYG1vZGVsX291dGxyQ2AuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhpcyBsaW5lYXIgbW9kZWwgc2hvdWxkIGV4cGxhaW4gYHlgIGJhc2VkIG9uIGB4YCB3aGljaCBpcyBmb3VuZCBpbiB0aGUgZGF0YWZyYW1lIGBvdXRsckNgLlwiKVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwicmlcIiwgdW5kZWZpbmVkX21zZz1cIk1ha2Ugc3VyZSB0byBleHRyYWN0IHRoZSByZXNpZHVhbHMgdG8gdGhlIHZhcmlhYmxlIGByaWAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiWW91IGNhbiBleHRyYWN0IHRoZSBzdGFuZGFyZGl6ZWQgcmVzaWR1YWxzIGJ5IHVzaW5nIGByc3RhbmRhcmRgIG9uIGBtb2RlbF9vdXRsckNgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsaW5kZXg9MSwgbm90X2NhbGxlZF9tc2c9XCJVc2UgdGhlIGBzdW1tYXJ5YCBmdW5jdGlvbiB0byB2aWV3IHRoZSBzdW1tYXJ5IG9mIGByaWAuXCIpICU+JSBjaGVja19hcmcoLiwgXCJvYmplY3RcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc3BlY2lmeSB0aGF0IHdlIHdhbnQgdG8gbG9vayBhdCB0aGUgc3VtbWFyeSBvZiBgcmlgLlwiKVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwiaGlpXCIsIHVuZGVmaW5lZF9tc2c9XCJNYWtlIHN1cmUgdG8gZXh0cmFjdCB0aGUgbGV2ZXJhZ2UgdmFsdWVzIHRvIGEgdmFyaWFibGUgbmFtZWQgYGhpaWAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiWW91IGNhbiBleHRyYWN0IHRoZSBsZXZlcmFnZSB2YWx1ZXMgYnkgdXNpbmcgdGhlIGBoYXR2YWx1ZXNgIGZ1bmN0aW9uIG9uIGBtb2RlbF9vdXRsckNgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsaW5kZXg9Miwgbm90X2NhbGxlZF9tc2c9XCJVc2UgdGhlIGBzdW1tYXJ5YCBmdW5jdGlvbiB0byB2aWV3IHRoZSBzdW1tYXJ5IG9mIGBoaWlgLlwiKSAlPiUgY2hlY2tfYXJnKC4sIFwib2JqZWN0XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRoZSBzcGVjaWZ5IHRoYXQgd2Ugd2FudCB0byBsb29rIGF0IHRoZSBzdW1tYXJ5IG9mIGBoaWlgLiBcIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwicGxvdFwiLGluZGV4PTIsIG5vdF9jYWxsZWRfbXNnPVwiUGxlYXNlIHVzZSBgcGxvdGAgdG8gY3JlYXRlIGEgcGxvdCBvZiB0aGUgc3RhbmRhcmRpemVkIHJlc2lkdWFscyB2ZXJzdXMgdGhlIGxldmVyYWdlcy4gXCIpICU+JSB7XG4gIGNoZWNrX2FyZyguLCBcInhcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJXZSB3b3VsZCBsaWtlIHRoZSBsZXZlcmFnZXMgdG8gYmUgb24gdGhlIGhvcml6b250YWwgYXhpcy4gXCIpXG4gIGNoZWNrX2FyZyguLCBcInlcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJXZSB3b3VsZCBsaWtlIHRoZSBzdGFuZGFyZGl6ZWQgcmVzaWR1YWxzIHRvIGJlIG9uIHRoZSB2ZXJ0aWNhbCBheGlzLiBcIilcbn1cbnN1Y2Nlc3NfbXNnKFwiRXhjZWxsZW50ISBXaXRoIG9ubHkgdHdvIHZhcmlhYmxlcywgd2UgY291bGQgYXJndWUgZ3JhcGhpY2FsbHkgdGhhdCBvYnNlcnZhdGlvbnMgd2VyZSB1bnVzdWFsLiBJbiB0aGlzIGV4ZXJjaXNlLCB3ZSBzaG93ZWQgaG93IHN0YXRpc3RpY3MgY291bGQgYWxzbyBiZSB1c2VkIHRvIGlkZW50aWZ5IHVzdWFsIG9ic2VydmF0aW9ucy4gQWx0aG91Z2ggbm90IHJlYWxseSBuZWNlc3NhcnkgaW4gYmFzaWMgbGluZWFyIHJlZ3Jlc3Npb24sIHRoZSBtYWluIGFkdmFudGFnZSBvZiB0aGUgc3RhdGlzdGljcyBpcyB0aGF0IHRoZXkgd29yayByZWFkaWx5IGluIGEgbXVsdGl2YXJpYXRlIHNldHRpbmcuXCIpIiwiaGludCI6IlRoZXJlIGlzIG5vdGhpbmcgdG8gY2hhbmdlIGluIHRoZSBzYW1wbGUgY29kZS4gU2ltcGx5IHBsYXkgYXJvdW5kIHdpdGggdGhlIGNvZGUgdG8gZmlndXJlIG91dCB3aGF0IGV4YWN0bHkgaXQgZG9lcy4ifQ==

4.4.3 Exercise. High leverage and risk manager survey

Assignment Text

In a prior exercise, we fit a regression model of logcost on logsize, indcost and a squared version of indcost. This model is summarized in the object mlr_survey2. In this exercise, we examine the robustness of the model to unusual observations.

Instructions

Use the R functions rstandard() and hatvalues() to extract the standardized residuals and leverages from the model fitted. Summarize the distributions graphically.
You will see that there are two observations where the leverages are high, numbers 10 and 16. On looking at the dataset, these turn out to be observations in a high risk industry. Create a histogram of the variable indcost to corroborate this.
Re-run the regression omitting observations 10 and 16. Summarize this regression and the regression in the object mlr_survey2, noting differences in the coefficients.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNzdXJ2ZXkgPC0gcmVhZC5jc3YoXCJDU1ZEYXRhXFxcXFJpc2tfc3VydmV5LmNzdlwiLCBoZWFkZXI9VFJVRSlcbnN1cnZleSA8LSByZWFkLmNzdihcImh0dHBzOi8vYXNzZXRzLmRhdGFjYW1wLmNvbS9wcm9kdWN0aW9uL3JlcG9zaXRvcmllcy8yNjEwL2RhdGFzZXRzL2RjMWM1YmNlNDNlZjA3NmFhNzcxNjlhMjQyMTE4ZTJlNThkMDFmODIvUmlza19zdXJ2ZXkuY3N2XCIsIGhlYWRlcj1UUlVFKVxuc3VydmV5JGxvZ2Nvc3QgPC0gbG9nKHN1cnZleSRmaXJtY29zdClcbm1sci5zdXJ2ZXkyIDwtIGxtKGxvZ2Nvc3QgfiBsb2dzaXplICsgcG9seShpbmRjb3N0LDIpLCBkYXRhID0gc3VydmV5KSIsInNhbXBsZSI6Im1sci5zdXJ2ZXkyIDwtIGxtKGxvZ2Nvc3QgfiBsb2dzaXplICsgcG9seShpbmRjb3N0LDIpLCBkYXRhID0gc3VydmV5KVxuIyBFeHRyYWN0IHRoZSBzdGFuZGFyZGl6ZWQgcmVzaWR1YWxzIGFuZCBsZXZlcmFnZXMgZnJvbSB0aGUgbW9kZWwgZml0dGVkLiBTdW1tYXJpemUgdGhlIGRpc3RyaWJ1dGlvbnMgZ3JhcGhpY2FsbHkuXG5yaSA8LSBfX18obWxyLnN1cnZleTIpXG5oaWkgPC0gX19fKG1sci5zdXJ2ZXkyKVxucGFyKG1mcm93PWMoMSwgMikpXG5oaXN0KHJpLCBuY2xhc3M9MTYsIG1haW49XCJcIiwgeGxhYj1cIlN0YW5kYXJkaXplZCBSZXNpZHVhbHNcIilcbmhpc3QoaGlpLCBuY2xhc3M9MTYsIG1haW49XCJcIiwgeGxhYj1cIkxldmVyYWdlc1wiKVxuXG4jIENyZWF0ZSBhIGhpc3RvZ3JhbSBvZiB0aGUgdmFyaWFibGUgYGluZGNvc3RgXG5wYXIobWZyb3c9YygxLCAxKSlcbmhpc3QoX19fLCBuY2xhc3M9MTYpXG5cbiMgUmUtcnVuIHRoZSByZWdyZXNzaW9uIG9taXR0aW5nIG9ic2VydmF0aW9ucyAxMCBhbmQgMTYuIFN1bW1hcml6ZSB0aGlzIHJlZ3Jlc3Npb24gYW5kIHRoZSByZWdyZXNzaW9uIGluIHRoZSBvYmplY3QgIGBtbHJfc3VydmV5MmAsIG5vdGluZyBkaWZmZXJlbmNlcyBpbiB0aGUgY29lZmZpY2llbnRzLlxubWxyLnN1cnZleTMgPC0gbG0oX19fIH4gbG9nc2l6ZSArIHBvbHkoaW5kY29zdCwyKSwgZGF0YSA9IHN1cnZleSwgc3Vic2V0ID0tYygxMCwxNikpXG5zdW1tYXJ5KG1sci5zdXJ2ZXkyKVxuc3VtbWFyeShtbHIuc3VydmV5MykiLCJzb2x1dGlvbiI6InJpIDwtIHJzdGFuZGFyZChtbHIuc3VydmV5MilcbmhpaSA8LSBoYXR2YWx1ZXMobWxyLnN1cnZleTIpXG5cbnBhcihtZnJvdz1jKDEsIDIpKVxuaGlzdChyaSwgbmNsYXNzPTE2LCBtYWluPVwiXCIsIHhsYWI9XCJTdGFuZGFyZGl6ZWQgUmVzaWR1YWxzXCIpXG5oaXN0KGhpaSwgbmNsYXNzPTE2LCBtYWluPVwiXCIsIHhsYWI9XCJMZXZlcmFnZXNcIilcbnBhcihtZnJvdz1jKDEsIDEpKVxuaGlzdChzdXJ2ZXkkaW5kY29zdCwgbmNsYXNzPTE2KVxubWxyLnN1cnZleTMgPC0gbG0obG9nY29zdCB+IGxvZ3NpemUgKyBwb2x5KGluZGNvc3QsMiksIGRhdGEgPSAgc3VydmV5LCBzdWJzZXQgPS1jKDEwLDE2KSlcbnN1bW1hcnkobWxyLnN1cnZleTIpXG5zdW1tYXJ5KG1sci5zdXJ2ZXkzKSIsInNjdCI6ImV4KCkgJT4lIGNoZWNrX29iamVjdChcInJpXCIsIHVuZGVmaW5lZF9tc2c9XCJQbGVhc2UgZXh0cmFjdCB0aGUgc3RhbmRhcmRpemVkIHJlc2lkdWFscyBmcm9tIGBtbHIuc3VydmV5MWAgaW50byBgcmlgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIllvdSBjYW4gZXh0cmFjdCB0aGUgc3RhbmRhcmRpemVkIHJlc2lkdWFscyBmcm9tIGEgbGluZWFyIG1vZGVsIGJ5IHVzaW5nIGByc3RhbmRhcmQoKWAuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJoaWlcIiwgdW5kZWZpbmVkX21zZz1cIlBsZWFzZSBleHRyYWN0IHRoZSBsZXZlcmFnZSB2YWx1ZXMgZnJvbSBgbWxyLnN1cnZleTFgIGludG8gYGhpaWAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiWW91IGNhbiBleHRyYWN0IHRoZSBsZXZlcmFnZSB2YWx1ZXMgZnJvbSBhIGxpbmVhciBtb2RlbCBieSB1c2luZyBgaGF0dmFsdWVzKClgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJwYXJcIixpbmRleD0xLG5vdF9jYWxsZWRfbXNnPVwidXNlIHRoZSBgcGFyYCBjb21tYW5kIHRvIGFsdGVyIHlvdXIgcGxvdCB3aW5kb3cuIFwiKSAlPiUgY2hlY2tfYXJnKC4sIFwibWZyb3dcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJ0byBjcmVhdGUsIDIgc2lkZS1ieS1zaWRlIGdyYXBocywgc2V0IG1mcm93IHRvIGJlIGMoMSwyKS4gXCIpXG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcImhpc3RcIixpbmRleD0xLCBub3RfY2FsbGVkX21zZz1cInVzZSBgaGlzdGAgdG8gY3JlYXRlIGEgaGlzdG9ncmFtIG9mIHRoZSBzdGFuZGFyZGl6ZWQgcmVzaWR1YWxzLiBcIikgJT4lIHtcbiAgY2hlY2tfYXJnKC4sIFwieFwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlBsZWFzZSBjcmVhdGUgYSBoaXN0b2dyYW0gdXNpbmcgdGhlIHN0YW5kYXJkaXplZCByZXNpZHVhbHMuIFwiKVxuICBjaGVja19hcmcoLiwgXCJuY2xhc3NcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJQbGVhc2Ugc2V0IHRoZSBudW1iZXIgb2YgY2xhc3NlcyB0byBiZSAxNi4gXCIpXG59XG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcImhpc3RcIixpbmRleD0yLCBub3RfY2FsbGVkX21zZz1cIlVzZSBgaGlzdGAgdG8gY3JlYXRlIGEgaGlzdG9ncmFtIG9mIHRoZSBsZXZlcmFnZSB2YWx1ZXMuXCIpICU+JSB7XG4gIGNoZWNrX2FyZyguLCBcInhcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJQbGVhc2UgY3JlYXRlIGEgaGlzdG9ncmFtIHVzaW5nIHRoZSBsZXZlcmFnZSB2YWx1ZXMuIFwiKVxuICBjaGVja19hcmcoLiwgXCJuY2xhc3NcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJQbGVhc2Ugc2V0IHRoZSBudW1iZXIgb2YgY2xhc3NlcyB0byBiZSAxNi4gXCIpXG59XG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcInBhclwiLGluZGV4PTIsIG5vdF9jYWxsZWRfbXNnPVwiUGxlYXNlIHJlc2V0IHRoZSBwbG90IHRvIGNvbnRhaW4gYSBzaW5nbGUgcGxvdC4gXCIpICU+JSBjaGVja19hcmcoLiwgXCJtZnJvd1wiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIlRvIGNoYW5nZSBiYWNrIHRvIGEgc2luZ2xlIHBsb3QsIHNldCBtZnJvdyB0byBiZSBjKDEsMSkuIFwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJoaXN0XCIsaW5kZXg9Mywgbm90X2NhbGxlZF9tc2c9XCJVc2UgYGhpc3RgIHRvIGNyZWF0ZSBhIGhpc3RvZ3JhbSBvZiBgaW5kY29zdGAuXCIpICU+JSB7XG4gIGNoZWNrX2FyZyguLCBcInhcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJQbGVhc2UgY3JlYXRlIGEgaGlzdG9ncmFtIG9mIGBpbmRjb3N0YC5cIilcbiAgY2hlY2tfYXJnKC4sIFwibmNsYXNzXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiUGxlYXNlIHNldCB0aGUgbnVtYmVyIG9mIGNsYXNzZXMgdG8gYmUgMTYuIFwiKVxufVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwibWxyLnN1cnZleTNcIix1bmRlZmluZWRfbXNnPVwiUGxlYXNlIGNyZWF0ZSBhIGxpbmVhciBtb2RlbCB3aGVyZSB3ZSBleGNsdWRlZCBvYnNlcnZhdGlvbnMgMTAgYW5kIDE2IG5hbWVkIGBtbHIuc3VydmV5M2AuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTW9kZWwgYGxvZ2Nvc3RgIGFzIGEgZnVuY3Rpb24gb2YgYGxvZ3NpemVgIGFuZCBgaW5kY29zdGAgc3F1YXJlZC4gWW91IGNhbiBleGNsdWRlIHRoZSB0d28gdmFsdWVzIGJ5IHVzaW5nIHRoZSBzdWJzZXQgYXJndW1lbnQgaW4gYGxtYC5cIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwic3VtbWFyeVwiLGluZGV4PTEsbm90X2NhbGxlZF9tc2c9XCJQbGVhc2UgdXNlIGBzdW1tYXJ5YCB0byB2aWV3IGEgc3VtbWFyeSBvZiBgbWxyLnN1cnZleTJgLlwiKSAlPiUgY2hlY2tfYXJnKC4sIFwib2JqZWN0XCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIHNwZWNpZnkgdGhhdCB3ZSB3b3VsZCBsaWtlIGEgc3VtbWFyeSBvZiBgbWxyLnN1cnZleTJgLlwiKVxuZXgoKSAlPiUgY2hlY2tfZnVuY3Rpb24oXCJzdW1tYXJ5XCIsaW5kZXg9Mixub3RfY2FsbGVkX21zZz1cIlBsZWFzZSB1c2UgYHN1bW1hcnlgIHRvIHZpZXcgYSBzdW1tYXJ5IG9mIGBtbHIuc3VydmV5M2AuXCIpICU+JSBjaGVja19hcmcoLiwgXCJvYmplY3RcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc3BlY2lmeSB0aGF0IHdlIHdvdWxkIGxpa2UgYSBzdW1tYXJ5IG9mIGBtbHIuc3VydmV5M2AuXCIpXG5zdWNjZXNzX21zZyhcIkV4Y2VsbGVudCEgWW91IHdpbGwgaGF2ZSBub3RlZCB0aGF0IGFmdGVyIHJlbW92aW5nIHRoZXNlIHR3byBpbmZsdWVudGlhbCBvYnNlcnZhdGlvbnMgZnJvbSBhIGhpZ2ggcmlzayBpbmR1c3RyeSwgdGhlIHZhcmlhYmxlIGFzc29jaWF0ZWQgd2l0aCB0aGUgYGluZGNvc3RgIHNxdWFyZWQgYmVjYW1lIGxlc3Mgc3RhdGlzdGljYWxseSBzaWduaWZpY2FudC4gVGhpcyBpbGx1c3RyYXRlcyBhIGdlbmVyYWwgcGhlbm9tZW5hOyBzb21ldGltZXMsIHRoZSAnc2lnbmljYW5jZScgb2YgYSB2YXJpYWJsZSBtYXkgYWN0dWFsbHkgZHVlIHRvIGEgZmV3IHVudXN1YWwgb2JzZXJ2YXRpb25zLCBub3QgdGhlIGVudGlyZSB2YXJpYWJsZS5cIikiLCJoaW50IjoiPGNvZGU+cnN0YW5kYXJkKCk8L2NvZGU+IGFuZCA8Y29kZT5oYXR2YWx1ZXMoKTwvY29kZT4gY2FuIGJlIHVzZWQgdG8gZXh0cmFjdCB0ZWggc3RhbmRhcmRpemVkIHJlc2lkdWFscyBhbmQgbGV2ZXJhZ2VzIGZyb20gYSBmaXR0ZWQgbW9kZWwuIn0=

4.5 Collinearity

In this section, you learn how to:

Define collinearity and describe its potential impact on regression inference
Define a variance inflation factor and describe its effect on a regression coefficients standard error
Describe rules of thumb for assessing collinearity and options for model reformulation in the presence of severe collinearity
Compare and contrast effects of leverage and collinearity

4.5.1 Video

Video Overhead Details

A Details. Collinearity

Collinearity, or multicollinearity, occurs when one explanatory variable is, or nearly is, a linear combination of the other explanatory variables.
- Useful to think of the explanatory variables as being highly correlated with one another.
Collinearity neither precludes us from getting good fits nor from making predictions of new observations.
- Estimates of error variances and, therefore, tests of model adequacy, are still reliable.
In cases of serious collinearity, standard errors of individual regression coefficients can be large.
- With large standard errors, individual regression coefficients may not be meaningful.
- Because a large standard error means that the corresponding t-ratio is small, it is difficult to detect the importance of a variable.

B Details. Quantifying collinearity

A common way to quantify collinearity is through the variance inflation factor (VIF).

Suppose that the set of explanatory variables is labeled $x_{1},x_{2},\dots,x_{k}$.
Run the regression using $x_{j}$ as the “outcome” and the other $x$’s as the explanatory variables.
Denote the coefficient of determination from this regression by $R_j^2$.
Define the variance inflation factor

\[ VIF_{j}=\frac{1}{1-R_{j}^{2}},\ \ \ \text{ for } j = 1,2,\ldots, k. \]

C Details. Options for handling collinearity

Rule of thumb: When $VIF_{j}$ exceeds 10 (which is equivalent to $R_{j}^{2}>90\%$), we say that severe collinearity exists. This may signal is a need for action.
Recode the variables by “centering” - that is, subtract the mean and divide by the standard deviation.
Ignore the collinearity in the analysis but comment on it in the interpretation. Probably the most common approach.
Replace one or more variables by auxiliary variables or transformed versions.
Remove one or more variables. Easy. Which One? is hard.
- Use interpretation. Which variable(s) do you feel most comfortable with?
- Use automatic variable selection procedures to suggest a model.

4.5.2 Exercise. Collinearity and term life

Assignment Text We have seen that adding an explanatory variable $x^2$ to a model is sometimes helpful even though it is perfectly related to $x$ (such as through the function $f(x)=x^2$). But, for some data sets, higher order polynomials and interactions can be approximately linearly related (depending on the range of the data).

This exercise returns to our term life data set Term1 (preloaded) and demonstrates that collinearity can be severe when introducing interaction terms.

Instructions

Fit a MLR model of logface on explantory variables education, numhh and logincome
Use the function vif() from the car package (preloaded) to calculate variance inflation factors.
Fit and summarize a MLR model of logface on explantory variables education , numhh and logincome with an interaction between numhh and logincome, then extract variance inflation factors.

Hint. If the car package is not available to you, then you could calculate vifs using the [lm()] function, treating each variable separately. For example

1/(1-summary(lm(education ~ numhh + logincome, data = Term1))$r.squared)

gives the education vif.

4.6 Selection criteria

In this section, you learn how to:

Summarize a regression fit using alternative goodness of fit measures
Validate a model using in-sample and out-of-sample data to mitigate issues of data-snooping
Compare and contrast SSPE and PRESS statistics for model validation

4.6.1 Video

Video Overhead Details

A Details. Goodness of fit

Criteria that measure the proximity of the fitted model and realized data are known as goodness of fit statistics.
Basic examples include:
- the coefficient of determination $(R^{2})$,
- an adjusted version $(R_{a}^{2})$,
- the size of the typical error $(s)$, and
- $t$-ratios for each regression coefficient.

A Details. Goodness of fit

A general measure is Akaike’s Information Criterion, defined as

\[ AIC = -2 \times (fitted~log~likelihood) + 2 \times (number~of~parameters) \]

For model comparison, the smaller the $AIC,$ the better is the fit.
This measures balances the fit (in the first part) with a penalty for complexity (in the second part)
It is a general measure - for linear regression, it reduces to

\[ AIC = n \ln (s^2) + n \ln (2 \pi) +n +k + 3 . \]

So, selecting a model to minimize $s$ or $s^2$ is equivalent to model selection based on minimizing $AIC$ (same k).

C Details. Out of sample validation

When you choose a model to minimize $s$ or $AIC$, it is based on how well the model fits the data at hand, or the model development, or training, data
As we have seen, this approach is susceptible to overfitting.
A better approach is to validate the model on a model validation, or test data set, held out for this purpose.

D Details. Out of sample validation procedure

1. Using the model development subsample, fit a candidate model.
1. Using the Step (ii) model and the explanatory variables from the validation subsample, “predict” the dependent variables in the validation subsample, $\hat{y}_i$, where $i=n_{1}+1,...,n_{1}+n_{2}$.
1. Calc the *sum of absolute prediction errors**

\[SAPE=\sum_{i=n_{1}+1}^{n_{1}+n_{2}} |y_{i}-\hat{y}_{i}| . \]

Repeat Steps (i) through (iii) for each candidate model. Choose the model with the smallest SAPE.

E Details. Cross - validation

With out-of-sample validation, the statistic depends on a random split between in-sample and out-of-sample data (a problem for data sets that are not large)
Alternatively, one may use cross-validation
- Use a random mechanism to split the data into k subsets, (e.g., 5-10)
- Use the first k-1 subsamples to estimate model parameters. Then, “predict” the outcomes for the kth subsample and use SAE to summarize the fit
- Repeat this by holding out each of the k sub-samples, summarizing with a cumulative SAE.
Repeat these steps for several candidate models.
- Choose the model with the lowest cumulative SAE statistic.

4.6.2 Exercise. Cross-validation and term life

Assignment Text

Here is some sample code to give you a better feel for cross-validation.

The first part of the randomly re-orders (“shuffles”) the data. It also identifies explanatory variables explvars.

The function starts by pulling out only the needed data into cvdata. Then, for each subsample, a model is fit based on all the data except for the subsample, in train_mlr with the subsample in test. This is repeated for each subsample, then results are summarized.

Show Code

# Randomly re-order data - "shuffle it"
n <- nrow(Term1)
set.seed(12347)
shuffled_Term1 <- Term1[sample(n), ]
explvars <- c("education", "numhh", "logincome")

## Cross - Validation
crossvalfct <- function(explvars){
  cvdata   <- shuffled_Term1[, c("logface", explvars)]
  crossval <- 0
  k <- 5
  for (i in 1:k) {
    indices <- (((i-1) * round((1/k)*nrow(cvdata))) + 1):((i*round((1/k) * nrow(cvdata))))
    # Exclude them from the train set
    train_mlr <- lm(logface ~ ., data = cvdata[-indices,])
    # Include them in the test set
    test  <- data.frame(cvdata[indices, explvars])
    names(test)  <- explvars
    predict_test <- exp(predict(train_mlr, test))
    # Compare predicted to held-out and summarize
    predict_err  <- exp(cvdata[indices, "logface"]) - predict_test
    crossval <- crossval + sum(abs(predict_err))
  }
  crossval/1000
}

crossvalfct(explvars)

Instructions

Calculate the cross-validation statistic using only logarithmic income, logincome.
Calculate the cross-validation statistic using logincome, education and numhh.
Calculate the cross-validation statistic using logincome, education, numhh and marstat.

The best model has the lowest cross-validation statistic.

eyJsYW5ndWFnZSI6InIiLCJwcmVfZXhlcmNpc2VfY29kZSI6IiNUZXJtIDwtIHJlYWQuY3N2KFwiQ1NWRGF0YVxcXFx0ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtIDwtIHJlYWQuY3N2KFwiaHR0cHM6Ly9hc3NldHMuZGF0YWNhbXAuY29tL3Byb2R1Y3Rpb24vcmVwb3NpdG9yaWVzLzI2MTAvZGF0YXNldHMvZWZjNjRiYzJkNzhjZjZiNDhhZDJjM2Y1ZTMxODAwY2I3NzNkZTI2MS90ZXJtX2xpZmUuY3N2XCIsIGhlYWRlciA9IFRSVUUpXG5UZXJtMSA8LSBzdWJzZXQoVGVybSwgc3Vic2V0ID0gZmFjZSA+IDApXG5UZXJtMSRtYXJzdGF0IDwtIGFzLmZhY3RvcihUZXJtMSRtYXJzdGF0KVxuXG5jcm9zc3ZhbGZjdCA8LSBmdW5jdGlvbihleHBsdmFycyl7XG4gIGN2ZGF0YSAgIDwtIHNodWZmbGVkX1Rlcm0xWywgYyhcImxvZ2ZhY2VcIiwgZXhwbHZhcnMpXVxuICBjcm9zc3ZhbCA8LSAwXG4gIGsgPC0gNVxuICBmb3IgKGkgaW4gMTprKSB7XG4gICAgaW5kaWNlcyA8LSAoKChpLTEpICogcm91bmQoKDEvaykqbnJvdyhjdmRhdGEpKSkgKyAxKTooKGkqcm91bmQoKDEvaykgKiBucm93KGN2ZGF0YSkpKSlcbiAgICAjIEV4Y2x1ZGUgdGhlbSBmcm9tIHRoZSB0cmFpbiBzZXRcbiAgICB0cmFpbl9tbHIgPC0gbG0obG9nZmFjZSB+IC4sIGRhdGEgPSBjdmRhdGFbLWluZGljZXMsXSlcbiAgICAjIEluY2x1ZGUgdGhlbSBpbiB0aGUgdGVzdCBzZXRcbiAgICB0ZXN0ICA8LSBkYXRhLmZyYW1lKGN2ZGF0YVtpbmRpY2VzLCBleHBsdmFyc10pXG4gICAgbmFtZXModGVzdCkgIDwtIGV4cGx2YXJzXG4gICAgcHJlZGljdF90ZXN0IDwtIGV4cChwcmVkaWN0KHRyYWluX21sciwgdGVzdCkpXG4gICAgIyBDb21wYXJlIHByZWRpY3RlZCB0byBoZWxkLW91dCBhbmQgc3VtbWFyaXplXG4gICAgcHJlZGljdF9lcnIgIDwtIGV4cChjdmRhdGFbaW5kaWNlcywgXCJsb2dmYWNlXCJdKSAtIHByZWRpY3RfdGVzdFxuICAgIGNyb3NzdmFsIDwtIGNyb3NzdmFsICsgc3VtKGFicyhwcmVkaWN0X2VycikpXG4gIH1cbiAgY3Jvc3N2YWwvMTAwMDAwMFxufSIsInNhbXBsZSI6IiMgUmFuZG9tbHkgcmUtb3JkZXIgZGF0YSAtIFwic2h1ZmZsZSBpdFwiXG5uIDwtIG5yb3coVGVybTEpXG5zZXQuc2VlZCgxMjM0NylcbnNodWZmbGVkX1Rlcm0xIDwtIFRlcm0xW3NhbXBsZShuKSwgXVxuXG4jIENhbGN1bGF0ZSB0aGUgY3Jvc3MtdmFsaWRhdGlvbiBzdGF0aXN0aWMgdXNpbmcgb25seSBsb2dhcml0aG1pYyBpbmNvbWUsIGBsb2dpbmNvbWVgLlxuZXhwbHZhcnMuMSA8LSBjKFwibG9naW5jb21lXCIpXG5jcm9zc3ZhbGZjdChleHBsdmFycylcblxuIyBDYWxjdWxhdGUgdGhlIGNyb3NzLXZhbGlkYXRpb24gc3RhdGlzdGljIHVzaW5nIGBsb2dpbmNvbWVgLCBgZWR1Y2F0aW9uYCBhbmQgYG51bWhoYC5cbmV4cGx2YXJzLjIgPC0gYyhcImVkdWNhdGlvblwiLCBcIm51bWhoXCIsIFwibG9naW5jb21lXCIpXG5jcm9zc3ZhbGZjdChfX18pXG5cbiMgQ2FsY3VsYXRlIHRoZSBjcm9zcy12YWxpZGF0aW9uIHN0YXRpc3RpYyB1c2luZyBgbG9naW5jb21lYCwgYGVkdWNhdGlvbmAsIGBudW1oaGAgYW5kIGBtYXJzdGF0YC5cbmV4cGx2YXJzLjMgPC0gYyhfX18pXG5jcm9zc3ZhbGZjdChleHBsdmFycykiLCJzb2x1dGlvbiI6IiMgUmFuZG9tbHkgcmUtb3JkZXIgZGF0YSAtIFwic2h1ZmZsZSBpdFwiXG5uIDwtIG5yb3coVGVybTEpXG5zZXQuc2VlZCgxMjM0NylcbnNodWZmbGVkX1Rlcm0xIDwtIFRlcm0xW3NhbXBsZShuKSwgXVxuIyBDcm9zcyAtIFZhbGlkYXRpb25cbmV4cGx2YXJzLjEgPC0gYyhcImxvZ2luY29tZVwiKVxuY3Jvc3N2YWxmY3QoZXhwbHZhcnMuMSlcbmV4cGx2YXJzLjIgPC0gYyhcImVkdWNhdGlvblwiLCBcIm51bWhoXCIsIFwibG9naW5jb21lXCIpXG5jcm9zc3ZhbGZjdChleHBsdmFycy4yKVxuZXhwbHZhcnMuMyA8LSBjKFwiZWR1Y2F0aW9uXCIsIFwibnVtaGhcIiwgXCJsb2dpbmNvbWVcIiwgXCJtYXJzdGF0XCIpXG5jcm9zc3ZhbGZjdChleHBsdmFycy4zKSIsInNjdCI6ImV4KCkgJT4lIGNoZWNrX29iamVjdChcImV4cGx2YXJzLjFcIix1bmRlZmluZWRfbXNnPVwiQ3JlYXRlIGFuIG9iamVjdCBuYW1lZCBgZXhwbHZhcnMuMWAgdGhhdCBpcyBlcXVhbCB0byBgbG9naW5jb21lYC5cIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJNYWtlIHN1cmUgdG8gc2V0IGBleHBsdmFycy4xYCB0byBiZSB0aGUgY2hhcmFjdGVyIHN0cmluZyBgbG9naW5jb21lYCBhcyBvcHBvc2VkIHRvIHRoZSB2YWx1ZXMgaW4gYGxvZ2luY29tZWAuXCIpXG5leCgpICU+JSBjaGVja19mdW5jdGlvbihcImNyb3NzdmFsZmN0XCIsaW5kZXg9MSxub3RfY2FsbGVkX21zZz1cIlV0aWxpemUgdGhlIGN1c3RvbSBidWlsZCBmdW5jdGlvbiBgY3Jvc3N2YWxmY3RgIHRvIGNhbGN1bGF0ZSB0aGUgY3Jvc3MtdmFsaWRhdGlvbiBzdGF0aXN0aWMgZm9yIGBleHBsdmFycy4xYC5cIikgJT4lIGNoZWNrX2FyZyguLCBcImV4cGx2YXJzXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiVGhlIG9ubHkgYXJndW1lbnQgdGhhdCB5b3UgbmVlZCB0byBzZXQgaW4gYGNyb3NzdmFsZmN0YCBpcyBgZXhwbHZhcnNgIHdoaWNoIHNob3VsZCBiZSBzZXQgZXF1YWwgdG8gYGV4cGx2YXJzLjFgLlwiKVxuZXgoKSAlPiUgY2hlY2tfb2JqZWN0KFwiZXhwbHZhcnMuMlwiLHVuZGVmaW5lZF9tc2c9XCJDcmVhdGUgYW4gb2JqZWN0IG5hbWVkIGBleHBsdmFycy4yYCB0aGF0IGlzIGVxdWFsIHRvIGBsb2dpbmNvbWVgLCBgbnVtaGhgLCBhbmQgYGxvZ2luY29tZWAuXCIpICU+JSBjaGVja19lcXVhbChpbmNvcnJlY3RfbXNnPVwiTWFrZSBzdXJlIHRvIHNldCBgZXhwbHZhcnMuMmAgdG8gYmUgdGhlIGNoYXJhY3RlciBzdHJpbmdzIGBsb2dpbmNvbWVgLCBgbnVtaGhgLCBhbmQgYGxvZ2luY29tZWAgYXMgb3Bwb3NlZCB0byB0aGUgdmFsdWVzIGluc2lkZSBvZiB0aG9zZSB2ZWN0b3JzLiBcIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwiY3Jvc3N2YWxmY3RcIixpbmRleD0yLG5vdF9jYWxsZWRfbXNnPVwiVXRpbGl6ZSB0aGUgY3VzdG9tIGJ1aWxkIGZ1bmN0aW9uIGBjcm9zc3ZhbGZjdGAgdG8gY2FsY3VsYXRlIHRoZSBjcm9zcy12YWxpZGF0aW9uIHN0YXRpc3RpYyBmb3IgYGV4cGx2YXJzLjJgLlwiKSAlPiUgY2hlY2tfYXJnKC4sIFwiZXhwbHZhcnNcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJUaGUgb25seSBhcmd1bWVudCB0aGF0IHlvdSBuZWVkIHRvIHNldCBpbiBgY3Jvc3N2YWxmY3RgIGlzIGBleHBsdmFyc2Agd2hpY2ggc2hvdWxkIGJlIHNldCBlcXVhbCB0byBgZXhwbHZhcnMuMmAuXCIpXG5leCgpICU+JSBjaGVja19vYmplY3QoXCJleHBsdmFycy4zXCIsdW5kZWZpbmVkX21zZz1cIkNyZWF0ZSBhbiBvYmplY3QgbmFtZWQgYGV4cGx2YXJzLjNgIHRoYXQgaXMgZXF1YWwgdG8gYGxvZ2luY29tZWAsIGBudW1oaGAsIGBsb2dpbmNvbWVgLCBhbmQgYG1hcnN0YXRgLlwiKSAlPiUgY2hlY2tfZXF1YWwoaW5jb3JyZWN0X21zZz1cIk1ha2Ugc3VyZSB0byBzZXQgYGV4cGx2YXJzLjNgIHRvIGJlIHRoZSBjaGFyYWN0ZXIgc3RyaW5ncyBgbG9naW5jb21lYCwgYG51bWhoYCwgYGxvZ2luY29tZWAsIGFuZCBgbWFyc3RhdGAgYXMgb3Bwb3NlZCB0byB0aGUgdmFsdWVzIGluc2lkZSBvZiB0aG9zZSB2ZWN0b3JzLiBcIilcbmV4KCkgJT4lIGNoZWNrX2Z1bmN0aW9uKFwiY3Jvc3N2YWxmY3RcIixpbmRleD0zLG5vdF9jYWxsZWRfbXNnPVwiVXRpbGl6ZSB0aGUgY3VzdG9tIGJ1aWxkIGZ1bmN0aW9uIGBjcm9zc3ZhbGZjdGAgdG8gY2FsY3VsYXRlIHRoZSBjcm9zcy12YWxpZGF0aW9uIHN0YXRpc3RpYyBmb3IgYGV4cGx2YXJzLjNgLlwiKSAlPiUgY2hlY2tfYXJnKC4sIFwiZXhwbHZhcnNcIikgJT4lIGNoZWNrX2VxdWFsKGluY29ycmVjdF9tc2c9XCJUaGUgb25seSBhcmd1bWVudCB0aGF0IHlvdSBuZWVkIHRvIHNldCBpbiBgY3Jvc3N2YWxmY3RgIGlzIGBleHBsdmFyc2Agd2hpY2ggc2hvdWxkIGJlIHNldCBlcXVhbCB0byBgZXhwbHZhcnMuM2AuXCIpXG5zdWNjZXNzX21zZyhcIkV4Y2VsbGVudCEgVGhpcyBleGVyY2lzZXMgZGVtb25zdHJhdGVzIHRoZSB1c2Ugb2YgY3Jvc3MtdmFsaWRhdGlvbiwgYSB2ZXJ5IGltcG9ydGFudCB0ZWNobmlxdWUgaW4gbW9kZWwgc2VsZWN0aW9uLiBUaGUgZXhlcmNpc2UgYnVpbGRzIHRoZSBwcm9jZWR1cmUgZnJvbSB0aGUgZ3JvdW5kIHVwIHNvIHRoYXQgeW91IGNhbiBzZWUgYWxsIHRoZSBzdGVwcyBpbnZvbHZlZC4gRnVydGhlciwgaXQgaWxsdXN0cmF0ZXMgaG93IHlvdSBjYW4gZGV2ZWxvcCB5b3VyIG93biBmdW5jdGlvbnMgdG8gYXV0b21hdGUgcHJvY2VkdXJlcyBhbmQgc2F2ZSBzdGVwcy5cIikiLCJoaW50IjoiVGhlIGZ1bmN0aW9uIFtzYW1wbGUoKV0gaXMgZm9yIHRha2luZyByYW5kb20gc2FtcGxlcy4gV2UgdXNlIGl0IHdpdGhvdXQgcmVwbGFjZW1lbnQgc28gaXQgcmVzdWx0cyBpbiBhIHJlLW9yZGVyaW5nIG9mIGRhdGEuIn0=